Рассмотрим прямую задачу, как задачу распределения ограниченных ресурсов с целевой функцией, подлежащей максимизации. Ниже приведены формулировки прямой и двойственной задачи.
Прямая задачаДвойственная задача
, 
,
, 
,
, 
.
Условия прямой задачи можно интерпретировать следующим образом. Коэффициент 
- прибыль, приходящаяся на единицу продукции 
- го вида производственной деятельности. Расход ресурса 
, запасы которого ограничены величиной 
, на единицу продукции - го вида равен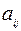 
единицам этого ресурса.
Переменные двойственной задачи 
интерпретируются как внутренняя (теневая) цена единицы ресурса (поэтому их иногда называют теневыми ценами). Они могут быть использованы для определения приоритета используемых ресурсов в соответствии с их вкладом в величину целевой функции 
, представляющую собой суммарную ценность ресурсов.
Сумму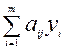 
можно рассматривать как суммарную оценку всех ресурсов - го способа производства. Ограничения двойственной задачи можно интерпретировать следующим образом:
Глава 3. ТРАНСПОРТНАЯ ЗАДАЧА (ТЗ)
