Рассмотрим прямую задачу ЛП.
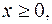
(2.7.1)
Двойственной задачей ЛП для прямой задачи (2.7.1) является:
(2.7.2)
Обозначим 
- 
-ю строку матрицы 
и 
- 
-й столбец матрицы . Пусть строки матрицы определяют коэффициенты отдельных ограничений прямой задачи. Тогда двойственная задача определяется следующим образом:
Прямая задача 
| Двойственная задача 
|
| 
|
| 
|
| 
|
| 
|
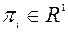
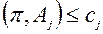
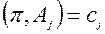
Следующие теоремы устанавливают взаимосвязь прямой и двойственной задач.
Теорема 5. Если прямая задача ЛП имеет оптимальное решение, то двойственная задача также имеет оптимальное решение, при этом значения их целевых функций равны.
Теорема 6. Задача, двойственная к двойственной задаче ЛП, совпадает с прямой задачей ЛП.
Теорема 7. Если дана пара, состоящая из прямой и двойственной задач ЛП, то возможна одна из трех ситуаций, отображенных в следующей таблице.
 Двойственная
Прямая
| конечный оптимум | неограничена | недопустима |
| Конечный оптимум | – | – | |
| Неограничена | – | – | |
| Недопустима | – |
