1) Градиент. Линейное локальное приближение. Скалярная функция f(x),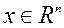 
, (краткая запись 
) называется дифференцируемой в точке х, если найдётся вектор 
, называемый градиентом функции такой, что
, 
,
Где 
обозначается величина, удовлетворяющая соотношению 
при 
.
Иначе можно сказать, что функция дифференцируема в точке х, если она допускает линейную аппроксимацию первого порядка в этой точке, т.е. найдётся линейная функция 
такая, что 
. Градиент определяется однозначно, при этом 
. Величина
называется производной по направлению функции f(x) в точке x.
2) Вторые производные. Квадратичное представление. Скалярная функция f(x) на 
называется дважды дифференцируемой в точке x, если она дифференцируема в этой точке и найдется симметричная 
матрица 
, называемая матрицей вторых производных (матрицей Гессе или гессиан), такая, что
, 
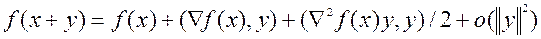Иначе говоря, функция дважды дифференцируема в точке х, если она допускает квадратичную аппроксимацию второго порядка в окрестности этой точки, т.е. существует квадратичная функция
такая, что 
.
Глава 2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ (ЛП)
Методы линейного программирования оказались эффективным средством решения задач области исследования операций. Слово «программирование» здесь соответствует слову «планирование». Методами ЛП можно решить многие задачи эффективного использования ресурсов.
Рассмотрим простой пример задачи планирования производства.
(максимизация прибыли),
(ограничение на ресурс досок) (2.0.1)
(ограничение на ресурс машинного времени).
Здесь: 
- количество выпускаемых в неделю двух видов полок; коэффициенты первого ограничения - затраты количества досок на единицу продукции каждого вида; коэффициенты второго ограничения - затраты количество машинного времени; правые части ограничений - максимально возможное количество ресурсов (досок и машинного времени); Функция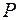 
- еженедельная общая прибыль, коэффициенты которой - прибыль от единицы продукции каждого вида. Это типичная двухмерная задача ЛП.
На рис.1. границы ограничений определяются прямыми:
, 
. (2.0.2)
Стрелки указывают области, где выполняются ограничения. Неотрицательность переменных задаёт неравенства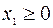 
, 
. Допустимая область заштрихована. Штриховыми линиями изображены прямые 
, 
, обозначенные 
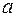и 
соответственно. Эти прямые параллельны и представляют собой две линии уровня функции 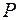со значениями 0 и 800. Градиент 
указывает направление возрастания.
Линией уровня с наибольшим значением 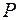, имеющей хотя бы одну общую точку с допустимой областью, является прямая, проходящая через вершину 
. Вершину можно найти, как точку пересечения двух прямых, решая систему уравнений (2.0.2) 
. Подставляя решение в 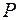найдем 
максимальную прибыль.
Рис. 1.
