Рассмотрим некоторые из примеров задач оптимизации.
1) Оценка параметров и структуры математической модели. Задачи поиска оптимума возникают, например, при построении математических моделей. Когда для изучения какого-либо явления конструируется математическая модель, к оптимизации прибегают для того, чтобы определить ее структуру и параметры, которые обеспечивают наилучшее согласование с реальностью.
Пусть результат измерения случайной величины 
зависит от 
, причем
,
где 
- результат измерения, 
- функция, вид которой известен,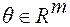 
- неизвестные параметры функции. Оценка неизвестных параметров 
при определенных условиях может быть произведена, например, по методу наименьших квадратов посредством минимизации суммы квадратов
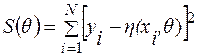
по . Здесь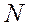 
- количество наблюдений.
Для определения структуры модели, т.е. определение ее вида, создается множество альтернативных моделей, среди которых выбирается одна из моделей по некоторому критерию. В качестве критерия может выступать либо сумма квадратов 
, либо оценка дисперсии модели.
2) Распределение ресурсов в условиях неполной информации. Пусть имеется 
ресурсов в количествах, задаваемых компонентами 
, 
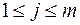, вектора 
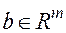. Обозначим 
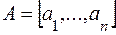матрицу размера 
. Столбец 
– матрицы A характеризует затраты ресурсов на единицу интенсивности 
-го способа производства. Обозначим 
вектор, компоненты которого 
, 
, -го способа производства, а 
вектор, компоненты которого 
, 
, доход от единицы продукции 
-го способа производства. Обозначим 
- общий доход. В принятых обозначениях задача распределения ресурсов между способами производства с целью максимизации дохода имеет вид:
, 
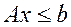. (1.2.1)
Для некоторых практических задач такая детерминированная модель не адекватна реальности, так как 
, 
случайные величины. Предположим, что с - случайный вектор с математическим ожиданием 
и ковариационной матрицей V. Тогда значение целевой функции z будет случайной величиной с математическим ожиданием 
и дисперсией 
.
Для максимизации ожидаемого значения z следует решить задачу
, 
.
Если требуется минимизировать дисперсию показателя z, то необходимо решить задачу
, 
, 
.
В реальных задачах возникает потребность получения максимального дохода при малых значениях дисперсии. Это многокритериальная задача, которая в некоторых постановках может быть сведена к однокритериальной задаче.
В следующей постановке требуется достигнуть лишь заданного уровня дохода 
при минимуме дисперсии.
, 
, 
, .
Другой подход может состоять в минимизации вероятности недостижения заданного уровня дохода.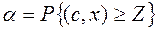 
. Пусть 
, где d, f -детерминированные векторы, а y - случайная составляющая. Тогда
.
Максимизация 
сводится к решению задачи:
, .
В том случае, когда с - случайный вектор, в зависимости от степени неприятия риска k, производится максимизация ожидаемого значения полезности
, 
, .
Приведенная функция полезности учитывает степень риска, связанную со случайным характером величины вектора дохода с, и основана на функции полезности индивида:
и предположении нормального закона распределения вектора c. Последняя функция при увеличении или уменьшении дохода z на величину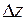 
более существенно реагирует на уменьшение дохода.
