Предположим, что решение задачи (2.7.1) мы начинаем с таблицы, в левой части которой стоит единичная матрица (см. рис.2). На произвольной итерации симплекс-метода мы имеем таблицу, где на месте единичной матрицы стоит матрица 
,где 
- матрица, составленная из столбцов исходной матрицы 
, соответствующих текущему БДР (см. рис.3).
| 
| |||||
|
|
рис.2. Исходная таблица. рис.3. Таблица текущей итерации
Нулевая строка текущей таблицы симплекс-метода, согласно (2.4.7), задается вектором
(2.8.1)
где вектор 
состоит из компонент вектора 
, соответствующих базисным столбцам 
. Используя факт, что решение двойственной задачи (2.7.2) 
где 
- соответствует оптимальному решению прямой задачи, из (2.8.1) получим
(2.8.2)
Учитывая, что левая часть матрицы A является единичной матрицей, запишем первые m компонент вектора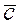 
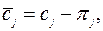
Отсюда следует, что решение двойственной задачи может быть получено на основе информации заключительной таблицы симплекс-метода
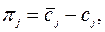
В заключение отметим, что на произвольном шаге симплекс-метода для базисных столбцов выполняется соотношение
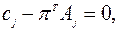
(2.8.3)
которые можно использовать для нахождения коэффициентов 
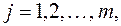для формирования нулевой строки. В некоторых задачах, например, транспортной, нулевая строка формируется на основе коэффициентов 
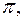вычисленных в результате решения системы (2.8.3).
