Решение задачи ЛП (2.1.1), согласно теоремам 2, 3, 4, достигается в вершине многогранного множества. Теорема 2 дает простое описание вершин и способ их определения при известном базисе. Число вершин конечно. Минимум задачи может быть найден за конечное число шагов посредством перебора вершин.
В симплекс-методе осуществляется идея перебора вершин соседних текущей вершине и выбора среди них в качестве следующего приближения вершины с наименьшим значением целевой функции. Симплекс-метод применяют для задач, записанных в форме:
. (2.4.1)
Пусть на 
-ом шаге получена точка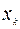 
, являющаяся вершиной множества 
, и пусть 
.
Назовем 
невырожденной вершиной множества , если число положительных компонент в ней равно 
.
Предположим, что все вершины множества невырождены. В силу невырожденности множество 
содержит элементов. Разобьем вектор 
на две группы 
, где 
отвечает компонентам из , 
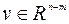- компонентам, не принадлежащим . Тогда система 
может быть записана в виде:
, (2.4.2)
где 
, столбцы которой являются столбцами 
с индексами из , 
-матрица, составленная из оставшихся столбцов. Отсюда, в силу невырожденности матрицы 
,
(2.4.3)
Целевая функция приобретает вид:
, (2.4.4)
где 
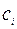- вектор с компонентами 
, 
, 
-вектор с компонентами 
, 
. С учетом (2.4.3) целевая функция может быть выражена только через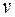 
.
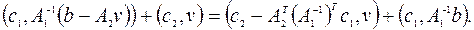
Следовательно, исходная задача эквивалентна следующей:
, 
(2.4.5)
При этом точке 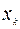соответствует вектор 
, где 
, 
. Точка является допустимой для задачи (2.4.5) при ограничении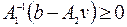 
, которое удовлетворяется как строгое неравенство 
. Поэтому оно может быть отброшено (как неактивное) при анализе точки 
на оптимальность.
В задаче
, 
(2.4.6)
минимум достигается в 0 тогда и только тогда, когда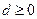 
.
Итак, если
(2.4.7)
то точка 
является решением (2.1.1) и одновременно (2.4.5), а тем самым 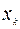является решением (2.4.1). Если же среди компонент 
есть отрицательные (например, 
), то не является решением (2.4.6), и, увеличивая 
, можно уменьшить значение целевой функции в (2.4.6).
Итак, сделаем шаг
- 
-й орт. (2.4.8)
Выбор 
производится из следующих соображений. С увеличением целевая функция уменьшается, однако может нарушиться ограничение 
, которое в точке , было неактивным. Итак, нужно выбрать из условия
. (2.4.9)
Если при этом 
, то задача не имеет решения в силу бесконечного убывания функции. Если же 
, то получаем новую точку 
,
где 
. Эта точка вновь является вершиной (она допустима и имеет m положительных компонент, так как -я компонента стала положительной, а одна из компонент 
обратилась в 0).
Поэтому в ней можно повторить всю процедуру заново. При этом значение целевой функции уменьшилось. Следовательно, возврат в одну из точек невозможен. В силу конечности общего числа вершин метод конечен.
Условия (2.4.7) являются условием оптимальности в симплекс-методе.
