В задаче (1.1.1) – (1.1.3) различают точки минимума двух видов.
Точка 
называется точкой локального минимума, если 
, где 
- e-окрестность точки 
, 
.
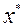Точка 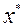называется точкой глобального минимума, если 
.
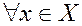Множество 
называется компактным, если любая последовательность 
имеет, хотя бы одну предельную точку . Известно, что всякая ограничённая последовательность имеет хотя бы одну предельную точку. Поэтому в 
компактным является любое замкнутое ограниченное множество.
Следующая теорема даёт достаточные условия существование оптимального решения задачи (1.1.1)-(1.1.3).
Теорема 1 (Вейерштрасса). Для того чтобы в задаче (1.1.1)-
(1.1.3) существовала точка глобального минимума, достаточно, чтобы допустимое множество 
было компактно, а целевая функция 
непрерывна на .
В силу сложности проверки ограниченности множества X, а зачастую, в силу его неограниченности, на практике часто применяется:
Следствие (теоремы Вейерштрасса). Если функция f непрерывна в и 
, то достигает своего глобального минимума в любом замкнутом подмножестве .
