При использовании «исправленного» или «модифицированного» методов Эйлера по сравнению с методом Эйлера для получения каждой новой точки приходится вычислять
значение функции f (x, y) уже дважды - в точках ( ) и (
) и (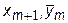 ) или (
) или ( ) и (
) и ( ), т.е. за повышение точности приходится расплачиваться дополнительными затратами машинного времени.
), т.е. за повышение точности приходится расплачиваться дополнительными затратами машинного времени.
Более высокая точность может быть достигнута, если пользователь готов потратить дополнительное машинное время на еще лучшую аппроксимацию производной путем сохранения большего числа членов ряда Тейлора. Эта идея лежит в основе методов Рунге-Кутта. Собственно, усовершенствованный и модифицированный методы Эйлера являются методами Рунге-Кутта 2-го порядка.
Чтобы удержать в ряде Тейлора член n -го порядка, необходимо каким-то образом вычислить n -ую производную зависимой переменной. При использовании модификаций метода Эйлера для получения второй производной в конечно-разностной форме достаточно было знать наклоны кривой на концах рассматриваемого интервала. Чтобы вычислить третью производную в конечно-разностном виде, необходимо знать значение второй производной по меньшей мере в двух точках. Для этого необходимо дополнительно определить наклон кривой в некоторой промежуточной точке интервала h, т.е. между xm и ym. Oчевидно, чем выше порядок вычисляемой производной, тем больше дополнительных вычислений потребуется внутри интервала. Метод Рунге-Кутта дает набор формул для расчета координат внутренних точек, требуемых для реализации этой идеи. Так как существует несколько способов расположения внутренних точек и выбора относительных весов для найденных производных, то метод Рунге-Кутта в сущности объединяет целое семейство методов решения дифференциальных уравнений первого порядка.
Наиболее распространенным из них является метод, при котором удерживаются все члены, включая h 4. Это метод четвертого порядка точности, для которого ошибка на шаге имеет порядок h 5. Расчеты при использовании этого классического метода производятся по формуле
 , ,
| (7.13) |
| где | K 0 = h f (xm, ym), |
| K 1 = h f (xm +0.5 h, ym +0.5 K 0), | |
| K 2 = h f (xm +0.5 h, ym +0.5 K 1), | |
| K 3 = h f (xm + h, ym + K 2). |
По сравнению с методами Эйлера и его модификациями метод Рунге-Кутта четвертого порядка имеет важное преимущество, так как обеспечивает более высокую точность, которая с лихвой оправдывает дополнительное увеличение объема вычислений.






