Обыкновенное дифференциальное уравнение порядка n имеет вид:
| (7.1) |
где 
)- производные первого, второго,..., n -го порядков от искомой функции y. Его решением является семейство функций
y = y (x, a 1, a 2,..., a n),
где a 1, a 2,..., a n - произвольные константы.
Например, простейшее дифференциальное уравнение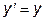 
имеет решение y = a ex (рис.7.1). Каждому какому угодно значению параметра a соответствует своя функция, и все эти функции удовлетворяют исходному уравнению.
Рис.7.1. Семейство кривых - решение
дифференциального уравнения y ' = y
| 
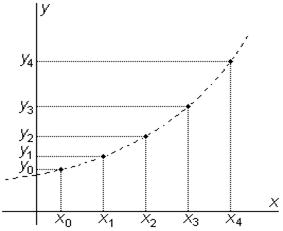Рис.7.2. Результат численного решения
задачи Коши
|
Если в дополнение к уравнению (7.1) задать конкретные значения
для некоторого значения x 0 в виде
 ;  ;  ;...;  ,
| (7.1’) |
то тем самым определяется конкретный набор a 1, a 2,..., a n и, следовательно, единственная конкретная функция y (x, a 1, a 2,..., a n) из всего семейства решений.
Условия (7.1') называются начальными условиями, а вся задача, включающая дифференциальное уравнение (7.1) и начальные условия (7.1'), называется "задачей Коши".
Класс дифференциальных уравнений, позволяющих аналитическими методами получить решение, довольно узок. Например, уравнение y ' = x 2 + y 2 не имеет аналитического решения. В большинстве практических задач функция F или коэффициенты, входящие в нее, могут содержать существенные нелинейности или даже задаваться в виде таблиц экспериментальных данных, и тогда аналитическое решение задачи Коши становится невозможным.
При численном решении задачи Коши необходимо задаваться границами x нач, x кон изменения аргумента x и величиной h, являющейся шагом его изменения, который определяет дискретность вычисления значений функции y = y (x).
Решение, полученное численным методом, есть таблица соответствующих значений (x i, y i), i = 0,1,2,..., n, где x 0= x нач, x n= xкон; x i+1 = xi + h.
