Данные методы относятся к простейшим из класса методов Ньютона-Котеса. В них подынтегральная функция f (x) на каждом интервале разбиения заменяется полиномом нулевой степени, т.е. константой. Такая замена является неоднозначной, т.к. константу можно выбрать равной значению f (x) в любой точке данного интервала разбиения.
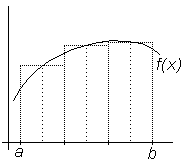
В любом случае значение частичного интеграла определяется как произведение длины интервала разбиения на выбранную константу, т.е. как площадь прямоугольника. В зависимости от способа выбора аппроксимирующей константы различают методы левых, средних или правых прямоугольников (рис.6.4).
Левые
| 
Средние
|  Правые
|
Рис.6.4. Геометрическая интерпретация методов прямоугольников
Введем следующие обозначения: точку a на оси OX обозначим через x 0, точку b - через x n, а точки разбиения промежутка [ a,b ] - через x 1, x 2,..., x n-1. Предполагается, что длина интервала разбиения постоянна на всем [ a,b ]. Обозначим ее через h:
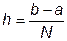; x i = x i-1 + h, i =1,2,..., N.
Тогда в методе левых прямоугольников площадь каждого i -го прямоугольника
| S i = h f (x i), i = 0,1,2,..., n -1, | (6.2) |
а для всего промежутка [ a,b ]: 
