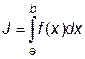 ,
| (6.1) |
где f (x) - подынтегральная функция, непрерывная на [ a,b ];
a,b - нижний и верхний пределы интегрирования.
Геометрически вычисление определенного интеграла интерпретируется как вычисление площади, ограниченной осью OX и графиком f (x) на промежутке [ a,b ] изменения х (рис.6.1).
К численному вычислению интеграла (численному интегрированию) обращаются в случаях, когда невозможно аналитически записать первообразную интеграла:
через элементарные функции или если такая запись имеет очень сложный вид.
| 
Геометрическая
интерпретация определенного
интеграла
|
Суть большинства методов численного интегрирования состоит в замене подынтегральной функции f (x) аппроксимирующей функцией 
, для которой можно легко записать первоообразную в элементарных функциях, т.е.
,
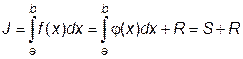где S - приближенное значение интеграла (6.1);
R - погрешность численного вычисления интеграла J.
