В этом методе подынтегральная функция f(x) на интервале [xi,xi+1] заменяется полиномом первой степени, т.е. наклонной прямой линией. Обычно эта прямая проводится через значения f(x) на границах интервала (рис.6.6). В этом случае приближенное значение частичного интеграла определяется площадью трапеции:
Рис.6.6. Геометрическая
интерпретация метода
трапеций
|  ,
т.е.  ,
а численное значение интеграла на всем [a,b]
 .
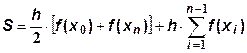Это вычислительная формула метода трапеций.
| (6.12) (6.13) |
Выражение для главного члена погрешности частичного интеграла:
.
Тогда главный член полной погрешности метода трапеций имеет вид
 ,
| (6.18) |
т.е. метод трапеций имеет также второй порядок, но его погрешность в два раза больше, чем в методе средних прямоугольников, поэтому, если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка использовать метод средних прямоугольников.