Аппроксимация зависимостей методом наименьших квадратов

В практике обработки экспериментальных данных могут быть ситуации, когда применение лагранжевой аппроксимации (полиномиальной или сплайновой) не оправдано или в принципе невозможно. Первым примером такой ситуации могут служить случаи, когда набор экспериментальных данных был получен со значительной погрешностью, либо на измеряемую (зависимую) величину влияли некоторые дополнительные, не учитываемые факторы. Для демонстрации этой ситуации на рис.5.5 представлены экспериментальные точки, истинная неизвестная кривая f(x) и аппроксимирующая кривая (x), полученная одним из методов лагранжевой аппроксимации. Второй пример, представленный на рис.5.6, демонстрирует ситуацию, когда экспериментальные замеры в каждом узле проводились неоднократно и, вследствие погрешности измерительных приборов либо каких-либо других факторов, дали разные результаты. В этом случае применение лагранжевой аппроксимации в принципе невозможно, так как каждому узлу x_i соответствует несколько разных значений f_i.

В этих условиях требуется проводить аппроксимирующую кривую, которая не обязательно проходит через узловые точки, но в то же время отражает исследуемую зависимость и сглаживает возможные выбросы, возникшие из-за погрешности эксперимента.

Рис.5.5.

Рис.5.6.

Как и в описанных выше методах аппроксимации считаем известными значения экспериментальных данных в узлах f(x _i) = f _i и через (x) обозначим непрерывную аппроксимирующую функцию. В узлах значения функций f(x) и (x) будут отличаться на величину _i = f (x _i) - (x _i). Отклонения _i могут принимать как положительные, так и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат, а для оценки близости функций f(x) и (x) возьмем сумму этих квадратов

Q = = .

(5.11)

Метод построения аппроксимирующей функции (x) из условия минимума величины Q называется методом наименьших квадратов ( далее - МНК).

Наиболее распространен способ выбора функции (x) в виде линейной комбинации

(x) = с0 0(x) + с1 1(x) + … + сm m(x),

(5.12)

где ₀(x), ₁(x), …, _m(x) - базисные функции; ;

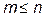с_0, с_1, …, с_m - коэффициенты, определяемые при минимизации величины Q.

Математически минимум величины Q достигается при равенстве нулю частных производных от Q по всем коэффициентам с_0, с_1, …, с_m:

	(5.13)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Эта система линейных алгебраических уравнений относительно неизвестных с_0, с_1, …, с_m называется системой нормальных уравнений, а матрица ее коэффициентов имеет следующий вид:

(5.14)

Элементы матрицы (5.14) являются скалярными произведениями базисных функций

.

(5.15)

Так как , то матрицу (5.14) можно переписать в виде

(5.16)

Матрица (5.16) называется матрицей Грама.

Расширенная матрица системы (5.13) получается добавлением справа к (5.16) сто­л­б­ца свободных членов

,

(5.17)

где - скалярные произведения. аналогичные (5.15).

При обработке экспериментальных данных, полученных с погрешностью в каждой узловой точке, обычно начинают с аппроксимации функцией , представленной одной-двумя базисными функциями. После определения коэффициентов с_k вычисляется ве­ли­чина Q по формуле (5.11). Если окажется, что , то необходимо расширить базис добавлением новых базисных функций . Расширение базиса необходимо про­­должать до тех пор, пока не выполнится условие .

Дата добавления: 2015-02-12; просмотров: 434 | Нарушение авторских прав | Изречения для студентов

Читайте также:

ПОЧЕМУ ПСИХИЧЕСКИ ЗДОРОВЫМ ЛЮДЯМ МОЖЕТ ПОНАДОБИТЬСЯ КОНСУЛЬТАЦИЯ СПЕЦИАЛИСТА

ПОЧЕМУ ССОРЫ ПРИЧИНЯЮТ БОЛЬ

Почему человеку так трудно принимать решения

ПОЧЕМУ ЖЕНЩИНЫ НЕ ОБРАЩАЮТСЯ С ПРОСЬБОЙ

Рекомендуемый контект:

Поиск на сайте:

© 2015-2020 lektsii.org - Контакты - Последнее добавление