При большом количестве узлов и, соответственно, при высокой степени аппроксимирующего полинома полиномиальная интерполяция не всегда дает удовлетворительные результаты, потому что в определенных ситуациях возникает так называемое "явление волнистости", из-за которого аппроксимирующая функция, несмотря на выполнение условий Лагранжа в узлах, может давать значительные отклонения от аппроксимируемой кривой между узлами. При этом повышение степени полинома приводит не к уменьшению, а к увеличению погрешности.
В этих условиях хороший эффект может дать интерполяция, основанная на теории сплайн-функций. Слово spline по-английски означает рейка, линейка. Этот термин возник из опыта работы чертежников, которые для проведения гладких кривых через точки на плоскости используют упругую линейку, совмещая ее с заданными точками. Из условий упругости недеформируемой линейки установлено, что между соседними узлами линейка проходит по линии, удовлетворяющей условию:
 IV(x) = 0, IV(x) = 0,
| (5.7) |
где  IV - четвертая производная от функции
IV - четвертая производная от функции  (x).
(x).
Самой простой кривой, удовлетворяющей этому условию, является полином третьей степени, поэтому в сплайновой аппроксимации наиболее распространенным является применение кубических сплайнов. В отличие от полиномиальной аппроксимации, когда вся аппроксимируемая функция описывается одним полиномом, при интерполяции кубическими сплайнами на каждом интервале [ x i-1, x i] строится отдельный полином третьей степени со своими коэффициентами. Как было отмечено выше, для однозначного построения кубической параболы необходимо задание четырех точек на плоскости. При построении каждого i-го сплайна (i=1,2,...,n) известны только две точки x i-1 и x i; поэтому кроме условий Лагранжа для этих точек
 , ,
| |
| (5.8) | |
 ; ;
| i = 1,2,...,n |
необходимо задание еще двух каких-то условий. Ими является "гладкость" перехода с одного полинома на соседний, выражаемая как непрерывность первой и второй производной от сплайнов в узлах:
 , ,
| |
| (5.9) | |
 ; ;
| i = 1,2,...,n-1. |
Условия (5.9) можно задать только для внутренних узловых точек таблицы x1,...,xn-1. Поэтому нужны еще дополнительные условия для концевых точек интервала аппроксимации x0 и xn. Обычно здесь используются условия свободных концов сплайнов (линейка не закреплена в точках вне интервала [ x0, xn] и, следовательно, описывается там уравнением прямой, т.е. полиномом первой степени). Значит для концов интервала должны выполняться условия
 = 0, = 0,
| |
| (5.10) | |
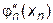 = 0. = 0.
|
Условия (5.8), (5.9), (5.10), расписанные для каждой узловой точки, дают систему из 4 n линейных алгебраических уравнений для определения коэффициентов всех n сплайнов (по 4 коэффициента на каждый сплайн). Данная система после некоторых преобразований приводится к так называемому трехдиагональному виду, т.е. ее матрица имеет ненулевые элементы только на главной диагонали и двух примыкающих к ней диагоналях. Для решения таких систем применяется специальный метод, называемый методом прогонки и являющийся частным случаем метода Гаусса.






