При выполнении прямого хода метода Гаусса при решении СЛАУ вычисление по формулам (4.15), (4.16) производится для j=1,..., n+1, т.е. преобразованию подлежат как коэффициенты при неизвестных x 1,..., xn, так и свободные члены системы.
Аналогичный алгоритм, но для j=1,...,n, может быть применен для вычисления определителя любой квадратной матрицы порядка n. Подставляя (4.15) в (4.16), получим:
 , ,
| (4.17) |
где k = 1,..., n-1 - номер шага преобразования матрицы; i = k+1,...,n; j = 1,2,...,n.
Так как i изменяется от k+1, то это означает, что первая строка матрицы не изменяется. Преобразование исходной матрицы по формуле (4.17) приводит к треугольной матрице, у которой элементы, расположенные ниже главной диагонали, равны нулю:

| 
| 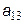
| ... | 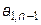
| 
|

| 
| ... | 
| 
| |

| ... | 
| 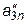
| ||
| ... | ... | ... | ... | ... | ... |
| ... | 
| 
| |||
| ... | 
|
Преобразование (4.17) является линейным и поэтому не приводит к изменению определителя матрицы; но так как преобразованная матрица - треугольная, то ее определитель равен произведению элементов главной диагонали. В отличие от решения СЛАУ здесь не требуется выполнение обратного хода.
Для получения максимальной точности результата надо стремиться, как и при решении СЛАУ, к тому, чтобы на каждом k-ом шаге преобразования на месте элемента а kk находился максимальный по модулю элемент из тех, что стоят в k-ом столбце ниже k-ой строки. Это достигается процедурой выбора главного элемента, поэтому при вычислении определителя надо учитывать, что перестановка любых двух строк матрицы приводит к изменению знака определителя на противоположный.




