Основной задачей линейной алгебры является решение систем линейных алгебраических уравнений (СЛАУ). Кроме этого здесь решаются задачи обращения матриц, вычисления определителей, нахождения собственных значений и собственных векторов матриц.
Общий вид системы линейных алгебраических уравнений:
| a11 x1 | + | a12 x2 | + | ... | + | a1n xn | = | a1,n+1 | |
| a21 x1 | + | a22 x2 | + | ... | + | a2n xn | = | a2,n+1 | (4.1) |
| .... | . | .... | . | ... | . | .... | . | .... | |
| an1 x1 | + | an2 x2 | + | ... | + | ann xn | = | an,n+1 |
где aij - заданные элементы расширенной матрицы СЛАУ (i=1,...,n, j=1,...,n+1);
xi - неизвестные (искомые) величины;
n - порядок системы.
Системе (4.1) соответствует расширенная матрица размера n на n+1:
| a11 | a12 | ... | a1n | a1,n+1 |
| a21 | a22 | ... | a2n | a2,n+1 |
| . | . | . | . | . |
| an1 | an2 | ... | ann | an,n+1 |
в которой первые n столбцов состоят из коэффициентов при неизвестных, а последний столбец образован из свободных членов системы (4.1).
Решить СЛАУ - значит найти такую комбинацию значений xi, при которой каждое уравнение (4.1) превращается в тождество.
По правилу Крамера каждое значение xi решения системы (4.1) вычисляется по формуле xi= D i /D, где D - определитель матрицы коэффициентов при неизвестных, D i - определитель матрицы, полученной из матрицы коэффициентов при неизвестных заменой i-го столбца на столбец свободных членов.
Этой формулой можно с успехом пользоваться для систем 2-го, 3-го порядков, но для более высоких порядков вычисление определителей становится довольно сложной проблемой, и поэтому метод, основанный на правиле Крамера, практически не используется.
4.2. Решение систем линейных алгебраических уравнений методом Гаусса
Значительно более простым и эффективным по быстродействию является метод Гаусса. Алгоритм этого метода состоит из двух этапов, называемых, соответственно, прямым и обратным ходом. Целью прямого хода является последовательное исключение неизвестных из уравнений системы; и только в обратном ходе производится непосредственное определение значений неизвестных.
Вначале рассмотрим выполнение алгоритма метода Гаусса на примере системы 3-го порядка
| a 11 x 1 | + | a 12 x 2 | + | a 13 x 3 | = | a 14 | |
| a 21 x 1 | + | a 22 x 2 | + | a 23 x 3 | = | a 24 | (4.1’) |
| a 31 x 1 | + | a 32 x 2 | + | a 33 x 3 | = | a 34 | . |
Из первого уравнения (4.1’) выразим x 1:
| x 1 = (a 14 - a 12 x 2 - a 13 x 3) / a 11 , | (4.2) |
а само это уравнение запишем в виде:
x 1 + 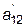 x 2 + x 2 +  x 3 = x 3 =  , ,
| (4.3) |
где
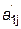 = a 1j / a 11, j = 2,3,4. = a 1j / a 11, j = 2,3,4.
| (4.4) |
Подставим (4.2) с учетом (4.4) во второе и третье уравнения (4.1’) и получим систему:
| x 1 | + |  x 2 x 2
| + |  x 3 x 3
| = | 
| |
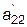 x 2 x 2
| + | 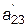 x 3 x 3
| = | 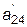
| (4.5) | ||
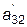 x 2 x 2
| + |  x 3 x 3
| = | 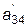
| , |
где 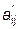 = a ij - a i1 .
= a ij - a i1 . 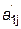 , i=2,3; j = 2,3,4,
, i=2,3; j = 2,3,4,
т.е. на данном этапе прямого хода из второго и третьего уравнений системы исключено неизвестное x 1.
Из второго уравнения преобразованной системы (4.5) выразим x 2 :
x 2 = (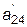 - - 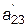 x 3) / x 3) /  , ,
| (4.6) |
а само это уравнение запишем в виде:
x 2 +  x 3 = x 3 =  , ,
| (4.7) |
где
 = = 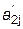 / / 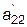 , j = 3,4. , j = 3,4.
| (4.8) |
Подставим (4.6) с учетом (4.8) в третье уравнение (4.5) и получим систему:
| x 1 | + | 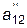 x 2 x 2
| + |  x 3 x 3
| = | 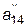
| |
| x 2 | + |  x 3 x 3
| = | 
| (4.9) | ||
 x 3 x 3
| = | 
| , |
где 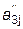 =
=  -
- 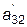 .
.  , j = 3,4,
, j = 3,4,
т.е. на данном этапе прямого хода из третьего уравнения системы исключено x 2.
Из третьего уравнения (4.9) выразим x 3: x 3 =  /
/  ,
,
или x 3 =  .
.
Теперь система приобретает вид:
| x 1 | + |  x 2 x 2
| + |  x 3 x 3
| = | 
| |
| x 2 | + |  x 3 x 3
| = | 
| (4.10) | ||
| x 3 | = | 
| . |
На этом заканчивается прямой ход метода Гаусса. Матрица коэффициентов полученной системы имеет вид:

| 
| ||

| (4.11) | ||
| . |
Это треугольная матрица. На ее главной диагонали расположены единицы, а элементы под главной диагональю равны нулю.
Обратный ход метода очевиден. Третье уравнение системы (4.10) уже явно определяет значение x 3
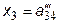 . .
| (4.12) |
Подставляя это значение во второе уравнение (4.10), получаем:
 . .
| (4.13) |
Подставляя найденные значения x 2, x 3 в первое уравнение (4.10), получаем значение x 1:
 . .
| (4.14) |
Соотношения (4.12), (4.13), (4.14) и являются решением системы (4.1’).
Теперь обобщим рассмотренный алгоритм на произвольную систему n-го порядка. На каждом k-ом шаге (k=1,2,3,...,n) прямого хода выполняются операции:
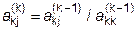 , ,
| j = 1,2,...,n+1, | (4.15) |
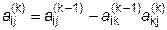 , ,
| i = k+1,...,n; j = 1,2,...,n+1. | (4.16) |
На последнем шаге, т.е. при k=n, выполняются только операции (4.15), так как для выполнения (4.16) уже исчерпаны все значения i.
При выполнении операций (4.15) производится деление на диагональные элементы a kk. Поэтому может возникнуть критическая ситуация, если этот элемент оказывается равным нулю. Избежать этой ситуации можно путем перестановки уравнений преобразуемой системы, начиная с k-го и по n-е таким образом, чтобы на месте a kk оказался ненулевой элемент. Более того, доказано, что для достижения максимальной точности решения системы надо перестановку уравнений осуществлять таким образом, чтобы на месте a kk оказывался максимальный по модулю элемент из тех, что находятся в k-м столбце матрицы системы начиная с диагонального и ниже. Эта процедура называется выбором главного элемента. Если же в результате этой процедуры на главной диагонали окажется все-таки нулевой элемент, то это означает, что главный определитель D матрицы системы равен нулю. По правилу Крамера это значит, что система вырожденная, т.е. либо не имеет решений, либо имеет их бесконечно много.






