Для хвилі типу Н складова 
. Підставимо в (11) та (12)
а)
(36)
б)
Знайдемо 
з (36)
i пiдставимо в (36)
, звiдси отримаємо
. (37)
Для того, щоб (37) привести до класичної форми, помножимо (37) зліва
на орт 
Тут маємо подвійний векторний добуток
, а тому
Скалярний добуток 
, бо кут між векторами z0 та HS дорівнює
, а скалярний добуток 
, бо кут дорівнює 0.
- звідси зразу отримаємо
(38)
Цей вираз показує, що поперечні складові HS та ES хвилі типу Н cинфазні та взаємно перпендикулярні.
З урахуванням (18)
отримаємо
, або
(39)
Для вакууму 
, 
, 
і з урахуванням цього
. (40)
Частотні залежності для 
зображені на рис. 1.6. Корисно порівняти їх з рис.1.4.
Рисунок 1.6 - Частотні залежності для
При 
опір 
- чисто уявна величина, вектори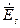 
та 
зсунуті по фазі на 
, передачі енергії нем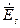а, та експоненціально зменшуються по z.
- залежність така ж, як і для хвилі типу Е.
Як видно з останніх виразів, хвиля Н також дисперсійна. Для подальшого розгляду нам буде потрібна гранична умова для складової Hz на поверхні ідеального провідника. Отримаємо її з виразу (36).
