Для прикладу розглянемо структуру е.м.п. для е.м.х. типу Еп (це найнижча хвиля типу Е); спочатку окремо по її складовим.
1. Структура Ez - співвідношення (56), рис. 2.2.
Хай умовно вектор Ez в перерізі z = z0 має напрям, який протилежний напряму вісі z - рис.2.2а.
Якщо розглянути переріз z = z0+ 
, то Ez міняє напрям на
протилежний, бо 
= -1 (дивись мал.2.2в).
Рисунок 2.2 - Структура складової Ez хвилі Еп
2. Структура Ех - (60а) та Ну - (60г), рис. 2.3а. та рис. 2.3б., відповідно, де позначкою (•) умовно зображено, що складова Ех переходить в складову
Рисунок 23 - Структура складових Ех та Н хвилі Еи
3. Структура Еg - (60б) та Нх - (60в), рис. 2.4а та 2.4б, відповідно.
Для побудування повної структури врахуємо, що:
1. Силові лінії вектора Е не перериваються, тобто силова лінія вектору Ez повинна замикатися силовими лініями 
;
2. Силові лінії вектора Hs повинні бути замкненими, тобто Нх повинно замикатися Ну;
3. В будь-якій точці поперечнього перерізу для отримання сумарного вектору треба скласти два вектора (векторно);
4. Максимуми (або мінімуми) поперечних та поздовжніх складових
вектору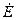 
зсунуті по вісі z на 
.
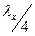Рисунок 2.4 - Структура складових Е та Нх хвилі Еп
Розглянемо відрізок хвилеводу з умовною довжиною 
та введемо характерні перерізи 1, 2, 3 - рис. 2.5.
Рисунок 2.5 - Характерні перерізи
Приймемо, що в розглядуваний момент часу t = t0 в перерізі z0 = 0 спостерігається максимум EzJ тобто Е2 = Ezmax.
Тоді з урахуванням зроблених зауважень (про побудування силових ліній для сумарних векторів) отримаємо повну структуру поля хвилі типу Еп - рис.2.6.
Рисунок 2.6 - Структура поля хвилі Е11 в перерізах
Далі розглянемо хвилі типу Н в прямокутному хвилеводі.
