Для будь якого типу хвиль при відсутності сторонніх джерел поля (або
струму, напруги, зарядів), вектори 
та 
задовольняють векторним рівнянням Гельмгольца:
, (4)
де 
- квадрат хвильового числа.
Рівняння (4) справедливо для будь якої хвилі.
Будемо шукати такі вирішення системи (4), які властиві біжучій хвилі, тобто у вигляді (2). Підставимо (2) в (4), та будемо вважати середовище без втрат, тобто 
, 
, а оператор Лапласа візьмемо у вигляді
,
де 
.
Тоді отримаємо
а) (5)
б)
Раніше в (4) множник 
був названий хвильовим числом. Але (4) - це рівняння відносно всіх трьох координат, а в (5) входять тільки дві поперечні координати ЛП, тому було б природнім назвати аналогічний множник в (5)
(4)
квадратом поперечнього хвильового числа (
) для відповідної ЛП. Тоді до
множника 
більше підійде назва: повздовжнє хвильове число вільного простору Кв. Таким чином далі будемо вважати
, 
, 
, (7)
де Кх - вільний простір;
- напрямна система.
З урахуванням співвідношення (1) кожне рівняння в (5а) та (5б) еквівалентне трьом скалярним рівнянням відносно Ех(х,у), Ez(x,y) та Нх(х,у), Ну(х,у) та Hz(x,y). Але розв'язувати шість рівнянь нема потреби, бо з рівнянь Максвелла можливо отримати вирази, які дають зв'язок між Es, Hs та Ez, Hz.
1.3 Зв'язок між Es, Hs тa Ez, Hz
Запишемо рівняння Максвелла в комплексній формі.
(8)
де 
.
Запишемо рівняння (8) відносно проекцій векторів 
, 
, , на вісі х та у
; 
;
; 
.
Далі врахуємо, що 
і тоді
а) (9)
б)
в)
г)
З виразу (9в) знайдемо 
(якщо 
, то і А = В).
- підставимо в (9а)
- знесемо 
вліво
- розділимо обидві частини на j та помножимо на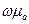 
і отримаємо вираз (10а).
Виконуючи аналогічні дії для 
, 
, 
неважко отримати (10б), (10в) та (10г)
 |
а)
б)
в) (10)
г)
Складемо (10а) та (10б) і отримаємо
.
Розглянемо вираз в останніх дужках з врахуванням векторних співвідношень 
; 
і отримаємо
,
або з врахуванням попереднього співвідношення
. (11)
Якщо скласти (10в) та (10г), неважко отримати
. (12)
Особливо відмітимо, що співвідношення (11) та (12) отримані з самих загальних співвідношень - рівнянь Максвелла, тому вони теж мають загальний характер, справедливі для будь-яких типів напрямлених хвиль - Е, Н, ТЕМ, гібридні та не залежать від типу ЛП.
Висновок: маючи співвідношення (11) та (12), для знаходження 
та 
достатньо вирішити (розв'язати) хвильові скалярні рівняння для 
та 
(а не вектори типу (4))
(13)
з граничними умовами, відповідними розглядуваному типу хвилі в конкретній ЛП, а потім поперечні складові знаходяться потім по (11) та (12).
