Розв'язок хвильового рівняння для складової 
Запишемо рівняння (13) в декартовій системі координат
(42)
Будемо розв'язувати це диференціальне рівняння другого порядку в частинних похідних методом розділення змінних, тобто представимо вирішення у вигляді:
(43)
В (34) X залежить від змінної х, a Y - від у. Підставимо (43) в (42) і отримаємо
Розділимо ліву та праву частини на 
(44)
В рівнянні (44) ліва частина уявляє собою суму двох незалежних по координатам х та у частин, тому можливо і праву частину представити у вигляді суми двох незалежних частин
(45)
тоді рівняння (45) розпадеться на два незалежних рівняння
; 
. (46)
Представимо (46) в іншому вигляді
; 
. (47)
Рівняння типу (36') добре вивчені. їх вирішення - це суперпозиція
гармонійних функцій
(48)
Підставимо (48) в (43) і отримаємо вирішення рівняння (42)
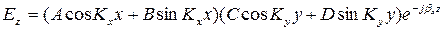(49)
Знаходження невідомих Кх, Ку та K 
В виразі (49) є шість невідомих: А, В, С, D, Кх, Ку. Для їх визначення
треба скористатися граничними умовами:
при х=0, х=а а)
(50)
при y=0, y=в б).
Підставимо (50а) в (49) і отримаємо два рівняння
а)
(51)
б).
Рівняння (51а) буде задовільнене при будь-яких значеннях змінної у тільки тоді, коли А=0. Підставимо А=0 в (51б) і отримаємо
Це рівняння буде при тій же умові (тобто для будь-яких у) задовільнене лише тоді, коли
BsinKxa = 0. (52)
Підставляючи (50б) в (49) аналогічно отримаємо
а)
б). (53)
Розглянемо сукупність рівнянь (52) та (53б). Вони при А=0 та С=0 можуть бути задовільнені лише тоді, коли
а)
(54)
б).
Якщо ж припустити, що для задовільнення (52) та (53а) величини B=D=0, то при А=С=0 отримаємо з співвідношення (49), що і Ez=0, а це не задовольняє головній умові існування хвилі типу 
.
Із (54) витікає, що
а)
(55)
б).
В (55) m та п - це натуральний ряд чисел, починаючи з 1, бо при А=С=0, значення m=0, або n=0 знову приводять до Ez = 0, тобто зникає хвиля типу Е. Підставимо А=0, С=0 та (55) в (49) і позначимо добуток BD = E0z.
. (56)
Таким чином, отримали вирішення хвильового рівняння (43) у вигляді
(56). Для знаходження поперечної сталої поширення 
підставимо (55)в (45) і отримаємо
(57)
Знаходження поперечних складових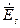 
та 
Для знаходження структури поперечних складових електричного поля 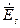та використаємо (11) та (12) при Hz = 0.
(58)
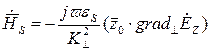(59)
Відмітимо, що (8') можливо і не користуватися, бо вже маємо співвідношення (32) для хвиль типу Е
Підставимо 
у вигляді (56) в (58)
З урахуванням 
, розпишемо останній вираз покоординатно
(60)
Використавши (32), із (60а), (60б) зразу ж отримаємо (урахувавши, що
(61)
Висновки по (56) та (60): 1. Структура 
, 
, 
, 
, 
в площині поперечнього перерізу відповідає структурі стоячих хвиль. При цьому m - число півхвиль, які вкладаються по широкій стінці, п - число стоячих півхвиль, які вкладаються по вузькій стінці. В відповідності до такої трактовки хвилі типу Е позначаються 
(або 
, або 
), де кожній парі індексів m та n відповідає своя структура е.м.х. в хвилеводі.
2. В напрямі вісі z всі складові для хвилі типу Е мають характер рухомої хвилі - залежність 
.
3. Залежність від часу - 
4. 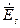та зсунуті по фазі відносно на 
, що в одиницях довжини відповідає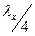 
, де 
- довжина хвилі в хвилеводі, яка визначається по (19).
5. Індекс 
, бо інакше Еz = 0 і зникає хвиля типу Е.
