Для хвиль типу Н ввели умову: 
Поздовжня складова магнітного поля Н2 задовільняє рівнянню (13)
Розпишемо оператор 
тоді рівняння буде
(62)
Приймемо, що 
і проведемо розділення змінних. Отримаємо вирішення
(63)
Для визначення невідомих А, В, С, D, Кх, Ку використаємо граничну умову (41) для Нz: 
=0.
З його використанням отримаємо:
B = 0; D = 0
(64)
(65)
Невідомі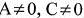 
, бо щезне хвиля Н при B=D=0 і звідси
(65)
З виразу (65) знайдемо
(66)
З виразу (66) виходить, що у хвиль типу Н при однакових з хвилями типу
Е значеннях індексів m та n значення параметрів 
співпадають
з аналогічними величинами для хвиль типу Е. Це явище зветься виродженням, а хвилі Н та Е при однакових m та n звуться виродженими хвилями. Позначаючи AC=Hoz і підставляючи знайдені невідомі в співвідношення (63), для Hz отримаємо
Для визначення поперечних складових використаємо (11) та (12)
(68)
Висновки по (67), (68).
1, 2, 3, 4 - тіж самі, що і для хвиль типу Е.
5. Індекси m та n можуть приймати значення m=0 або n=0, тобто хвиля типу Н може існувати і без півхвильових варіацій по вісям х або у для відповідних складових е.м.п. Таким чином, якщо a>b, то найнижчим типом хвилі серед хвиль типу Н є хвиля типу Н1о. Для неї 
. У найнижчої хвилі типу Е - хвилі Е11 
. Як видно 
, тому хвиля Н10 є найнижчою не тільки серед хвиль типу Н, а й серед хвиль типу Е, тобто серед всіх ймовірних типів хвиль прямокутного хвилевода.
