Для хвиль типу Е складова 
. Підставимо це значення в (11) та (12) і отримаємо
(31)
Знайдемо величину 
з (31а)
- підставимо в (246) і отримаємо
, a6o
. (32)
Як видно з (32) вектори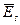 
та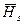 
взаємно перпендикулярні та синфазні, як і для хвилі ТЕМ. Підкреслимо, що це відноситься лише для поперечних складових.
Вже отримано (18) 
, де 
;
Підставимо (18) в (32)
.
Звідси зразу знайдемо zc з умови 
. (33)
Для вакууму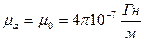 
, 
, тоді
, тоді
. (34)
Частотні залежності для 
зображені на рис. 1.4.
 |
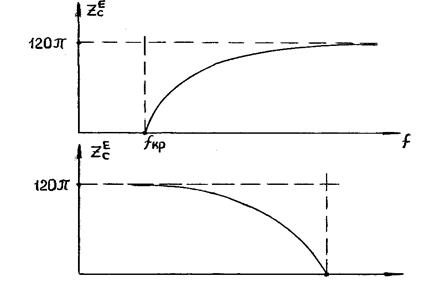Рисунок 1.4 - Частотні залежності для
При 
- чисто уявна величина, вектори 
та 
зсунуті по фазі на 
, 
, тому передачі енергії нема:
, тобто зменшується по закону експоненти. Підкреслимо, що це зменшення зумовлене не втратами в стінках, а реактивним характером е.м.х. в ЛП при
Знайдемо фазову швидкість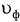 
хвилі типу Е.
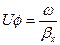- підставимо сюди (18) і отримаємо
,
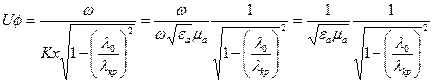Де 
- швидкість світла в середовищі з параметрами 
.
Частотні залежності для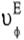 
зображені на рис. 1.5.
Рисунок 1.5 - Частотні залежності для 
Висновок: параметри хвилі типу Е нелінійно залежать від частоти, тобто ця хвиля дисперсійна.
