Для цієї хвилі по її визначенню Ez =0, Hz =0. Підставимо ці значення в (11) та (12) і отримаємо
. (20)
Оскільки завбачується, що хвиля існує, то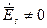 
, та 
, тоді з (20) виходить
, або 
, або fкр = 0 (21)
і, таким чином, в тих ЛП, де можливе існування ТЕМ- хвилі, вона може поширюватися на будь-яких частотах. Можливо показати, що цій умові в першу чергу задовольняють двозв'язані системи, тобто такі, де може існувати сталий струм (fкр =0). Поперечні перерізи таких ЛП зображені на рис. 1.3.
Рисунок 1.3- ЛП з хвилею ТЕМ
Для знаходження 
підставимо (21) в (18) і отримаємо
, (22)
звідси фазова швидкість
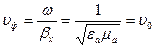, (23)
тобто 
та 
такі ж як і для плоскої хвилі в такому ж середовищі.
Підставимо в (5 вираз (22)
. (20)
Це рівняння Лапласа, які, як відомо, визначають потенціальні поля, а це, в свою чергу, визначає, що
, (25)
де 
- скалярний потенціал, який також задовольняє рівнянню Лапласа.
. (26)
Підкреслимо деякі важливі обставини:
1. Рівняння (24), (25) описують статичні поля і вони для хвилі з залежністю від
часу у вигляді 
справедливі лише тоді, коли зафіксувати час (t = t0).
2. Ці рівняння справедливі лише для поперечного перерізу, а по вісі z це 
.
Таким чином, розв'язавши (26), знайдемо 
, а потім по (25) знайдемо і 
. Функцію, яка аналогічна можливо ввести і для визначення 
- це векторний електродинамічний потенціал 
, але в цьому нема потреби, бо вектори 
та 
взаємозв'язані. Для того, щоб це продемонструвати підставимо в (9а)-(9г) значення Ez = 0, Hz = 0.
(27)
Зложимо (9б) з (9в) і отримаємо
.
З умови правої трійки знайдемо 
; 
, тоді
;
.
У відповідальності з (22) для хвилі ТЕМ 
, тоді
. (28)
Згадаємо визначення характеристичного опору для плоскої хвилі
- порівняємо з (28), звідси
, (29)
, (30)
Висновки:
1. З (29) виходить, що характеристичний опір хвилі ТЕМ для ЛП, що заповнена
речовиною з параметрами 
, 
співпадає з таким же для плоскої хвилі в середовищі з параметрами , .
2. З (30) виходить, що для хвилі ТЕМ вектори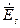 
та 
взаємно перпендикулярні.
3. Характеристики хвилі ТЕМ (, 
, Ккр, fкр, zc) не залежать від частоти. Але цей висновок справедливий лише до тої частоти fкр.в, починаючи з якої у відповідній ЛП можуть існувати хвилі більш високого типу, ніж ТЕМ - це Н, Е, гібридні.
