Гранична умова для Hz на поверхні провідника

 

Рисунок 1.7 - До граничної умови для складової H_z

 

З виразу (36) при E_z = 0 маємо .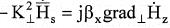

 

Але для будь-якої ЛП площина поперечнього перерізу перпендикулярна до вісі z, тобто будь-який орт буде лежати в цій площині, тому можливо за­писати, що

H_s = Нn, де n₀ - напрямок нормалі до бокової поверхні.

 

З другого боку, градієнт по S - це максимальна з похідних по напрямку, тобто

Таким чином

, але на поверхні провідника з .

Звідси витікає, що

. (41)

Порівняємо залежності та - рис.1.8.

Ці залежності навівають на думку, що на достатньо високих частотах сукупність хвиль Н та Е повинна дати хвилю типу ТЕМ.

Далі будемо розглядати конкретні напрямні системи, тобто лінії передавання різних типів. Почнемо з хвилеводів. Найбільш поширені з них мають поперечний переріз у формі прямокутника, або кола.

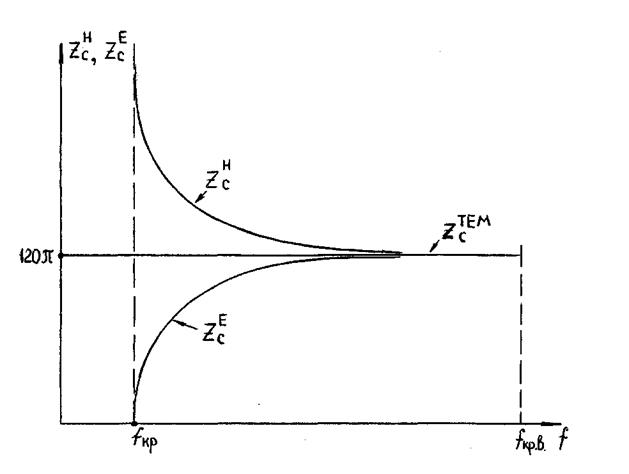
Рисунок 1.8 - До порівняння залежностей та

2 ПРЯМОКУТНИЙ ХВИЛЕВІД

Прямокутний хвилевід зображений на рис. 2.1

Рисунок 2.1 - Прямокутний хвилевід

 

Сумістимо початок декартової системи координат з вершиною внутрішнього кута хвилеводу - точка О. Хай розміри хвилеводу а та в.

Нагадаємо, що поздовжні складові E_z та Н_z задовольняють рівнянням (13)

 

(13)

а зв'язок між 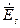, та , встановлюється виразами (11) та (12).

Будемо розглядати окремо хвилі типу Е та Н, а хвилі типу ТЕМ в таких системах поширюватися не можуть (бо нема умов для протікання сталого струму).