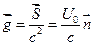По определению вектора потенциала

При дифференцировании по координате 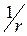 можно считать константой; Имеет место тождество
можно считать константой; Имеет место тождество 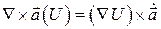
Рассмотрим распространение электромагнитных волн в вакууме, ограничившись лишь случаем монохроматической волны. Для нее получим:

Перейдем в этих формулах к пределу, считая 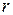 столь большим, что можно пренебречь различием в направлении векторов
столь большим, что можно пренебречь различием в направлении векторов  и
и 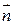 , где
, где  - единичный вектор, направленный из начала координат в точку наблюдения, а
- единичный вектор, направленный из начала координат в точку наблюдения, а 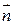 по-прежнему вектор, направленный от излучателя к точке наблюдения. Это означает, что
по-прежнему вектор, направленный от излучателя к точке наблюдения. Это означает, что  .
.
На достаточно больших расстояниях можно считать, что  и соответственно
и соответственно 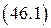 можно представить в виде:
можно представить в виде:
 ,
,
где  - волновой вектор, направленный по направлению распространения электромагнитной волны.
- волновой вектор, направленный по направлению распространения электромагнитной волны. 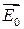 и
и 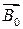 - постоянные векторы, причем подразумевается, что в окончательном выражении требуется брать вещественную часть. Векторы
- постоянные векторы, причем подразумевается, что в окончательном выражении требуется брать вещественную часть. Векторы  и
и 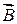 ортогональны к друг другу и вектору
ортогональны к друг другу и вектору  .
. 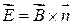 . Полученные формулы задают плоские монохроматические волны, т.к. плоскость
. Полученные формулы задают плоские монохроматические волны, т.к. плоскость 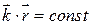 является поверхностью равной фазы, т.е. равных значений
является поверхностью равной фазы, т.е. равных значений  и
и 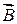 . Эти волны распространяются со скоростью
. Эти волны распространяются со скоростью  . Действительно, в момент времени
. Действительно, в момент времени 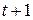 фазовый множитель имеет в точке
фазовый множитель имеет в точке 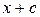 тоже значение, что имел в момент времени
тоже значение, что имел в момент времени 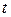 в точке
в точке 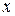 . Т.е.
. Т.е. 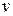 представляет собой скорость распространения поверхности равной фазы, т.е. фазовую скорость волны.
представляет собой скорость распространения поверхности равной фазы, т.е. фазовую скорость волны.
Вычислим вектор Поинтинга плоской волны:
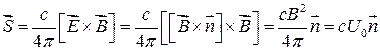 ,
,
где  .
.
Распространение плоских электромагнитных волн не сопровождается уменьшением их амплитуды и потока энергии, движущегося со скоростью света. Импульс плоской волны: