Ускоренно движущийся заряд теряет энергию на излучение. Т.к. поле обладает еще и импульсом, то излучение сопровождается обратным силовым воздействием поля на частицу, называемым реакцией излучения.
Баланс сил с учетом действия излучения:
,
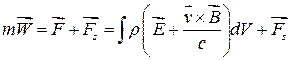где 
- внешняя сила, действующая на частицу, 
- сила реакции излучения или сила Лоренцова торможения.
Предположим, что 
, тогда в первом приближении заряд совершает движение под действием силы внешнего поля , а излучаемая мощность -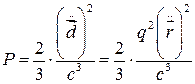 
. Допустим, что в момент времени 
заряд возвращается в исходное состояние движения, в котором он находился в момент времени 
. Рассмотрим баланс энергии для системы состоящей из заряда и внешнего электромагнитного поля. Если бы заряд ничего не излучал, то по возвращению в исходное состояние, то полная работа, совершенная над ним внешним полем, была бы нулевой. Значит изменение энергии внешнего поля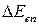 
=0. Если в следующем приближении учесть, что полная сила, действующая на заряд, складывается из и , то баланс энергии можно записать в виде:
Т.к. в силу сказанног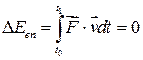о 
, то:
т.е:
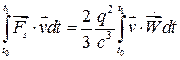, откуда
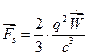
В силу сделанных предположений (), под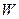 
надо понимать ускорение частицы во внешнем поле сил. В противном случае, если , мы имели бы уравнение:
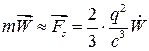, решение которого:
показывает, что под действием обратной реакции излучения ускорение экспоненциально возрастает - частица разгоняется. Это противоречит как законам механики, так и опытным данным. Так что и если 
- периодическая функция времени с частотой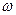 
, то:
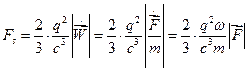
Условия применимости этого выражения () можно записать в виде
Это соотношение имеет фундаментальное значение. Классическая теория поля приводит к разумным результатам при выполнении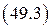 
или если ввести длину волны 
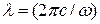лишь для волн 
.
Если под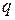 
и 
понимать заряд и массу электрона, то эти условия выполняются для всего оптического и рентгеновского излучения и не слишком жестких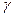 
- лучей. Величину 
см называют классическим радиусом электрона. Неравенство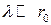 
интерпретируют следующим образом: у электромагнитных явлений масштаба порядка 
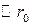реакция излучения становится немалой, по сравнению с другими силами и классическая теория не применима.
Замечание: фактическая область применимости классической теории поля еще уже. На расстояниях порядка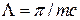 
начинают играть роль квантовые эффекты. 
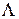называют комптоновской длиной волны. У электрона, например, 
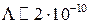см.
