Представим комплексную амплитуду в виде:
 , где
, где 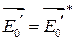 и
и 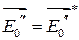 , тогда
, тогда
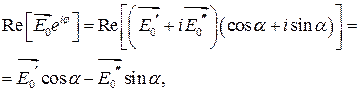
где 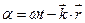 - доаза волны.
- доаза волны.
Перейдем от 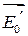 и
и  , которые могут иметь произвольную ориентацию к взаимно ортогональным векторам
, которые могут иметь произвольную ориентацию к взаимно ортогональным векторам  и
и  . Пусть:
. Пусть:
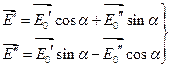
где  неизвестный угол, который следует найти. Тогда, требуя чтобы
неизвестный угол, который следует найти. Тогда, требуя чтобы 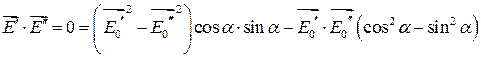 , находим:
, находим:

Выражая из 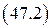
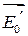 и
и  через
через  и
и  находим:
находим:
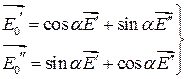
И используя  , получаем, что
, получаем, что
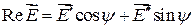 ,
, 
Пусть волна распространяется вдоль 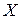 , а ось
, а ось 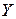 направлена
направлена  , тогда
, тогда  параллельна оси
параллельна оси  . Следовательно
. Следовательно  ,
, 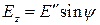 .
.  и
и  называются амплитудами, а
называются амплитудами, а 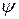 - фазой волны.
- фазой волны.
Поскольку 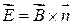 , то
, то 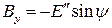 , а
, а 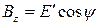 . Исключая фазу, находим, что
. Исключая фазу, находим, что
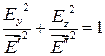
уравнение эллипса.
Таким образом, при  вектор
вектор 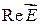 описывает эллипс в плоскости
описывает эллипс в плоскости 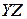 . Поэтому говорят, что плоская волна вообще говоря поляризована эллиптически. При распространении волны конец вектора
. Поэтому говорят, что плоская волна вообще говоря поляризована эллиптически. При распространении волны конец вектора 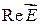 описывает эллиптическую спираль навитую на вектор
описывает эллиптическую спираль навитую на вектор 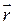 . Шаг этой спирали равен
. Шаг этой спирали равен  . В частном случае, когда
. В частном случае, когда  волна имеет круговую поляризацию. Если же
волна имеет круговую поляризацию. Если же  или
или  равно нулю - говорят о линейной поляризации. Необходимым и достаточным условием линейной поляризации является условие
равно нулю - говорят о линейной поляризации. Необходимым и достаточным условием линейной поляризации является условие  , а круговой -
, а круговой - 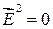 .
.






