где
Фурье спектры функций 
и 
для (1). 
, 
.
Формулы 
дают вещественное значение для 
и 
. В силу линейности производимых операций разложение выполняется как для промежуточных, так и для окончательных результатов. Например, дипольный и магнитный дипольный моменты примут вид:
Причем 
,и 
Используя эти функции, находим в дипольном приближении:
Учитывая, что
Де введен вектор 
, называется волновым вектором, а его модуль 
волновым числом. Используя эти обозначения находим:
Таким образом, полученные формулы дают спектральное разложение феерических волн на гармонические составляющие возможных частот, обусловленные соответствующими гармониками колебаний зарядов. Коэффициенты разложения в этих формулах
, 
зависят от частоты гармоник, направления, и величины вектора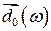 
и направления излучения. Спектральный состав излучения определяется набором частот излучений 
для дипольного и 
для магнитно-дипольного излучения при прочих равных условиях амплитуды вектора в поле пропорциональны 
, а потоки излучения пропорциональны 
. Это означает, что легче излучают высокочастотные осцилляторы. Строго монохроматическая волна испускается только строго гармоническим осциллятором. Любое отклонение от гармоничности дает излучение, занимающее некоторую полосу частот.
