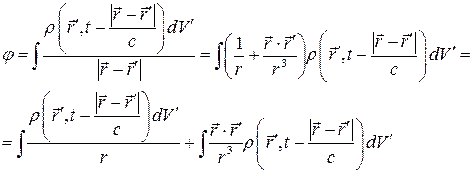
Ещё более упростить формулы для потенциалов можно, используя для 
приближение:
()
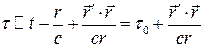При этом полное время запаздывания слагается из двух частей: Первая, 
, называемая временем запаздывания системы, представляет время распространения электромагнитного поля от начала координат до точки наблюдения. Вторая, 
, называемая собственным запаздыванием – это время, требующееся для распространения поля, в пределах системы. По порядку величины 
,так что при 
собственное запаздывание 
.
В принципе, плотность заряда можно разложить по малому параметру :
()
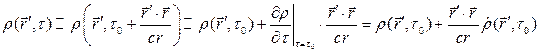При этом, однако, 
не должна являться быстро изменяющийся функцией своего аргумента, т.е. за врем я конфигурация зарядов в системе не должно успеть сильно измениться. За время заряды проходят путь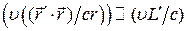 
.Если этот путь мал по сравнению с размерами системы, то есть
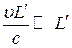или 
()
то разложение () правомерно.
Подставляя тогда () в () и ограничившись членами разложения с наименьшими степенями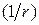 
получим
где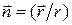 
.Слагаемое 
мало по сравнению с 
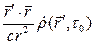на достаточно большом удалении от системы.
Т.к. в формуле все величины берутся в один и тот же момент времени, то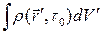 
- это просто полный заряд системы в момент времени 
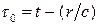. Для электронейтральной системы он равен нулю. В этом случае
()
Воспользовавшись уравнением непрерывности перепишем интеграл в правой части
Последний интеграл удобно вычислить в координатном представлении
где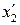 
и 
– границы области движения зарядов, на которой плотность тока обращается в ноль.
В векторном виде будем иметь
()
Подставляя () в () находим
()
Аналогично, для потенциала получаем
()
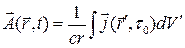Так что
()
Введем понятие дипольного момента 
системы зарядов:
()
Например, для системы состоящей из двух равных по величине и противоположных по знаку зарядов, 
, именуемой диполем
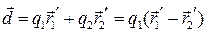
Теперь, используя определение (), мы видим, что
Здесь мы учили, что 
- переменная интегрирования, независимая от 
. Следовательно
()
()
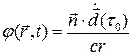Итак, в рассматриваемом приближении потенциалы поля вдали от системы определяются значением производной по времени от её дипольного момента. Поэтому такое приближение называется дипольным. Оно применимо при выполнении условия ().
Легко проверить, что в этом приближении потенциалы удовлетворяет калибровке Лоренца
Смысл полученных результатов прост: при движении зарядов в системе (изменений её дипольного момента) в окружающим пространстве возникает электромагнитном поле.
Потенциалы этого поля убывает по закону 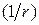, в то время как потенциалы электростатического поля по закону 
.
Система неравномерного движущихся зарядов является излучателем.
