Полученные в предыдущем параграфе формулу для мощности использовали при расчете ускорителей заряженных частиц. В ряде случаев потери на излучение является главным фактором, ограничив практически достижимую энергию в ускорителе. При заданной внешней силе, т.е скорости изменения импульса 
(обратно пропорциональна квадрату массы ускоряемой частицы), следовательно влияние этих радиационных эффектов максимально для электронов. Поэтому именно излучение электронов.
(1)
Конкретно, рассмотрим два случая:
1. 
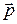не меняет направления (например, в линейных укорителях).
Тогда 
, следовательно 
(2)
Пусть движение происходит вдоль оси x, тогда
В дальнейшем будем писать 
, предполагая что E=E(x).
Вычислим отношение мощности, уходящей за счет излучения к подводимой мощности.
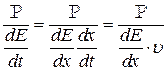
Получим
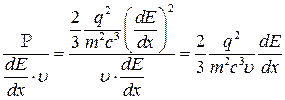
Рассмотрим релятивистский случай
для электрона, например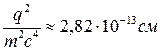 
, 
МэВ
Обычно измерения, т.е. 
энергии в линейных ускорителях 
.
Чтобы эффективно ускорять частицы, надо, чтобы потери мощности за счет излучения были малы по сравнению с подводимой мощностью. Для этого надо чтобы прирост энергии dE на расстояние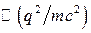 
было много меньше чем 
. В нашем случае 
. Из приведенных оценок ясно, что в линейных укорителях потери на излучение пренебрежительно малы.
2. 
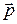, но направление быстро меняется (например, циклические ускорители,
типа синхротрона или бетатрона) излучение частиц в такого рода ускорителях называют синхротронными.
В таких ускорителях используются электромагнитные поля высокой частоты (СВЧ). Энергия частицы за один оборот изменяется мало, а направление 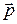- сильно.
Поэтому имеем
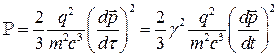(3)
Пусть частица движется равномерно по круговой орбите радиуса R с частотой 
, которой задается вектором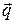 
.
Вводя оператор поворота на угол 
вокруг :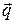
где в нашем случае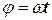 
, получаем, что
Пусть 
, тогда 
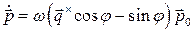
Следовательно:
(4)
Так как, 
, следовательно 
,
(5)
Основная формула для расчета мощности излучения в циклическом ускорителе.
За один период 
на излучение теряется энергия
(6)
Для больших электронных синхротронов 
максимальная энергия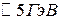 
.
При этом потери на излучение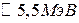 
за один оборот.
Практически очень трудно получить высококачественную мощность, обеспечивающую на много больший прирост мощности на обороте, так что энергия 5-10 ГэВ представляет верхний предел достижимых энергий в циклических электронных ускорителях.
