Если ускоренно движется заряд наблюдать из ИСО, в которой 
, то второе слагаемое, дающее вклад в излучение в (9) примет вид:
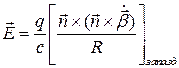(1)
Мгновенный поток энергии определяется вектором Пойтинга:
(
- вещественный вектор).
Вспоминая определение телесного угла:
, 
Находим, что мощность излучаемая в телесный угол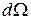 
равна
Следовательно
(2)
Используя формулу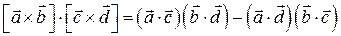 
Находим
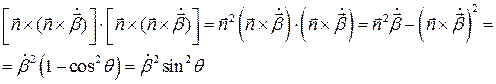
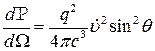(3)
Видно, что наибольшая мощность излучает движущий заряд отвечает 
Из формулы (1) следует, что вектор лежит в плоскости векторов 
и 
(излучение поляризована в плоскости , ).
Интегрируя (3) по всем телесным углам, находим полную мгновенную мощность излучения.
так как, 
, то 
, таким образом
(4)
Это известная нерелятивистская формула Лармора для ускоренно движущегося заряда.
Обобщим её на случай произвольно движущегося заряда. Так как. Энергия электромагнитного излучения при преобразованиях Лоренца ведет себя как четвертая (временная) компонента 4-вектора, то 
- инвариант преобразований Лоренца.
Если удастся найти инвариантное относительно преобразований Лоренца выражение, переходящее в (4) при 
, то это и будет требуемое обобщение. Конечно существует много величин, сводящих при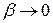 
к (4), но искомое выражение должно зависеть лишь от 
и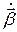 
. При таком ограничении, накладываемой на порядок производных, результат оказывается единственным.
Перепишем (4) в виде:
где m - масса заряженной частицы,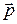 
- импульс.
Лоренц – инвариант обобщенного этого соотношения очевидно
(5)
где 
- собственное время 
, а 
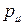- 4-вектор энергии импульса 
.
Очевидно, что отсюда следует
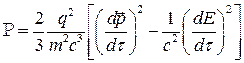(6)
Так как 
, 
(7), то 
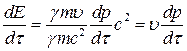, следовательно
(8)
Из последней формулы при 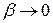действительно получаем формулу Лармора.
Выражая с помощью (7) все величины через скорость и ускорение, находим
, 
, 
(*) - 
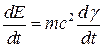
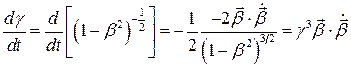
Формула Лиенара.
