Исследуйте на экстремум функцию 
.
Решение. Найдем экстремум функции, пользуясь первой производной. Данная функция определена и непрерывна на всей числовой прямой. Найдем производную, приравняем ее нулю и найдем критические точки. Имеем:
; 
следовательно, 
- критические точки. Теперь исследуем знак производной в окрестности каждой из этих точек.
|
при 
- функция убывает,
при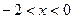 
- функция возрастает,
при 
- функция убывает,
при 
- функция возрастает.
Следовательно, 
- точка минимума, x=0- точка максимума, 
- точка минимума. Следовательно, имеем два минимума 
и максимум 
.
Найдите интервалы возрастания и убывания функций:
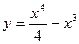
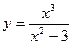
Найти экстремум функции и построить ее график
