Студенту необходимо научиться вычислять производные конкретных функций: y= x, y= 
и вообще y = 
.
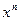Найдем производную функции у=х.
Имеем:
т.е. (x)′=1.
Найдем производную функции
Производная 
Пусть 
тогда
Легко заметить закономерность в выражениях производных от степенной функции 
при n=1,2,3.
Следовательно,
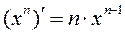. (1)
Эта формула справедлива для любых действительных n.
В частности, используя формулу (1), имеем:
;
.
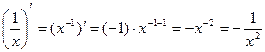Пример.
Найдите производную функции
.
Решение:
.
Данная функция является частным случаем функции вида
при 
.
Используя формулу (1), имеем
.
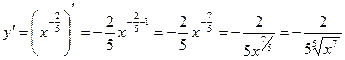Производные функций y=sin x и y=cos x.
Пусть y=sinx.
Разделим на ∆x, получим
Переходя к пределу при ∆x→0, имеем
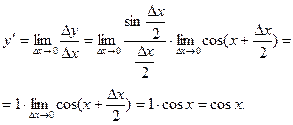
Пусть y=cosx.
Тогда
Отсюда
Переходя к пределу при ∆x→0, получим
; 
. (2)
