Пусть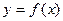 
(1)
есть дифференцируемая функция от аргумента x в некотором интервале (a,b).Если в уравнении (1) y рассматривать как аргумент,а x как функцию, то эта новая функция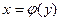 
, где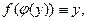 
называется,как мы знаем, обратной по отношению к данной.Нашей задачей является: зная производную 
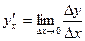функции 
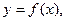найти производную 
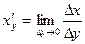обратной ей функции 
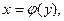предполагая,что обратная функция существует и непрерывна в соответствующем промежутке.
Теорема. Если для функции y=f(x)
существует обратная функция ,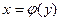
которая в рассматриваемой точке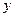 
имеет производную 
, отличную от нуля, то в соответствующей точке x функция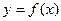 
имеет производную 
,
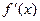равную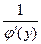 
, т.е. справедлива формула
Доказательство. Возьмем приращение ∆y,тогда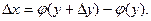 
Так как 
есть функция монотонная, то ∆x 
.
Рассмотрим тождество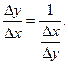 
Так как при ∆x→0 и ∆y→0,то 
т.е. 
