Пусть функция 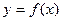 определена в некоторой окрестности точки
определена в некоторой окрестности точки 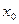
 , и непрерывна в точке
, и непрерывна в точке 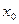 .
.
Пусть 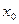 называется точкой максимума (минимума) функции, если существует такая окрестность точки
называется точкой максимума (минимума) функции, если существует такая окрестность точки 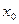
 , в которой при
, в которой при 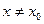 выполняется неравенство
выполняется неравенство 
 .
.
Точки максимума и минимума называются точками экстремума.
Необходимое условие точки экстремума:
В точках экстремума производная  или не существует.
или не существует.
Точки, в которых производная равна нулю или не существует, называются критическими точками.
Достаточные условия экстремума:
Пусть функция 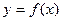 непрерывна в некоторой окрестности точки
непрерывна в некоторой окрестности точки 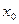 .
.
а) Если  при
при 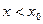 и
и 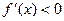 при
при  (т.е. при переходе через точку
(т.е. при переходе через точку 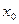 производная меняет
производная меняет
знак “+” на “–“), то точка 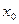 является точкой максимума.
является точкой максимума.
б) Если 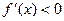 при
при 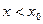 и
и  при
при  (т.е. при переходе через точку
(т.е. при переходе через точку 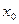 производная меняет знак “–” на “+“), то точка
производная меняет знак “–” на “+“), то точка 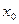 является точкой минимума.
является точкой минимума.
Пусть в критической точке 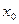 функция f(x) имеет вторую производную
функция f(x) имеет вторую производную  (значит,
(значит,  ). Если при этом
). Если при этом  , то
, то 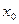 – точка максимума; если же
– точка максимума; если же 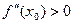 то
то 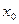 – точка минимума; если же
– точка минимума; если же  , то вопрос о наличии экстремума в этой точке остается открытым.
, то вопрос о наличии экстремума в этой точке остается открытым.
Функция f(x) называется возрастающей на отрезке [a; b], если для любых  и x
и x  на этом отрезке
на этом отрезке  , когда x
, когда x  < x
< x  .
.
Аналогично определяется убывание функции на отрезке.
Достаточные признаки возрастания и убывания функции y=f(x):
если 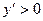 , то функция возрастает;
, то функция возрастает;
если  , то функция убывает.
, то функция убывает.
Чтобы найти экстремум функции нужно:
Найти  и критические точки, в которых
и критические точки, в которых  или не существует.
или не существует.
Определить знак 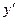 слева и справа от каждой критической точки.
слева и справа от каждой критической точки.
Далее можно найти  и
и  и построить кривую.
и построить кривую.






