Рассмотрим правила дифференцирования.
Теорема 1. Если функции u =u(x) и v=v(x) дифференцируемы в данной точке x,то в этой точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых: (u+v)'=u'+v'. (3)
Доказательство: рассмотрим функцию y=f(x)=u(x)+v(x).
Приращению ∆x аргумента x соответствуют приращения ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) функций u и v. Тогда функция y получит приращение
∆y=f(x+∆x)-f(x)=
=[u(x+∆x)+v(x+∆x)]--[u(x)+v(x)]=∆u+∆v.
Следовательно,
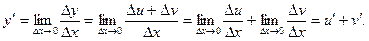
Итак, (u+v)'=u'+v'.
Теорема 2. Если функции u=u(x) и v=v(x) дифференцируемы в данной точке x, то в той же точке дифференцируемо и их произведение. При этом производная произведения находится по следующей формуле: (uv)'=u'v+uv'. (4)
Доказательство: Пусть y=uv, где u и v – некоторые дифференцируемые функции от x. Дадим x приращение ∆x;тогда u получит приращение ∆u, v получит приращение ∆v и y получит приращение ∆y.
Имеем y+∆y=(u+∆u)(v+∆v), или
y+∆y=uv+u∆v+v∆u+∆u∆v.
Следовательно, ∆y=u∆v+v∆u+∆u∆v.
Отсюда 
Переходя к пределу при ∆x→0 и учитывая, что u и v не зависят от ∆x, будем иметь


Теорема 3. Производная частного двух функций равна дроби, знаменатель которой равен квадрату делителя, а числитель- разности между произведением производной делимого на делитель и произведением делимого на производную делителя, т.е.
Если 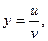 то
то 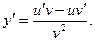 (5)
(5)
Теорема 4. Производная постоянной равна нулю, т.е. если y=C, где С=const, то y'=0.
Теорема 5. Постоянный множитель можно выносить за знак производной, т.е. если y=Cu(x), где С=const, то y'=Cu'(x).






