Найдите производную функции  .
.
Решение. Согласно формулам 5) и 7) имеем:

Найдите производные следующих функций:
1)  ; 9)
; 9) 
2) 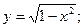 10)
10) 
3) 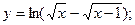 11)
11) 
4)  12)
12) 
5)  13)
13) 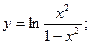
6) 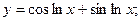 14)
14) 

7)  15)
15) 
8) 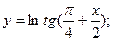 16)
16) 

Производные высших порядков.
Пусть функция y=f(x) в каждой точке интервала (a; b) имеет производную. Производную 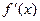 называют производной первого порядка или первой производной функции
называют производной первого порядка или первой производной функции 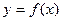 .
.
Рассмотрим функцию 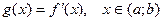 . Если g(x) имеет производную в точке
. Если g(x) имеет производную в точке 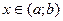 , то эту производную называют производной второго порядка или второй производной функции
, то эту производную называют производной второго порядка или второй производной функции 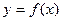 в точке х и обозначают
в точке х и обозначают  .
.
Коротко: вторая производная – это производная от первой производной, т.е.
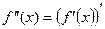 .
.
Аналогично определяется производная порядка n, где  .
.
Производной n-го порядка от функции 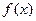 называется производная от производной (n-1)-го порядка и обозначается символом
называется производная от производной (n-1)-го порядка и обозначается символом 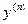 или
или 
Пример 1.
Если  , то
, то
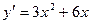 ;
;
 ;
;
 ;
;
 .
.






