Рассмотренные нами правила дифференцирования результатов арифметических действий не дают еще возможности вычислять производные от многих элементарных функций. Возьмем, например, функцию 
, которая не является ни суммой, ни произведением, ни частным более простых элементарных функций, и поэтому правила предыдущего параграфа к ней неприменимы. При этом является сложной функцией: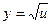 
, 
, и ее производную можно найти с помощью правила дифференцирования сложной функции, которое читается так.
Если функция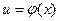 
имеет производную в точке x, а функция 
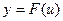имеет производную в точке 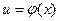, то сложная функция 
также имеет производную в точке x, причем 
.
Опуская аргумент и используя другое обозначение для производных, формулу можно переписать в виде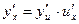 
.
Доказательство:
Придадим x приращение ∆x, оно вызовет приращение ∆u промежуточного аргумента u=φ(x),
которое в свою очередь повлечет изменение функции y на некоторую величину ∆y.
Для отыскания производной y′ нужно найти 
при∆x→0.
Представим отношение 
в виде
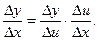
Тогда в силу правила предельного перехода в произведении получим:
(∆u→0 при ∆x→0, так как u=φ(x)- непрерывная функция).
Так как 
то мы приходим к доказанной формуле.
