Теорема Коши. Пусть функции 
и 
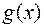удовлетворяют условиям: 1) непрерывны на 
; 2) дифференцируемы на 
; 3) 
на . Тогда существует точка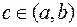 
такая, что справедлива формула:
. (1)
Доказательство. Рассмотрим вспомогательную функцию 
. Она непрерывна на и дифференцируема на . Подберем l так, чтобы 
:
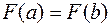. (2)
С таким l эта функция удовлетворяет условиям теоремы Ролля, следовательно 
: 
. Но 
, значит 
и
.
Сравнивая эту формулу с (2), получим (1).
Замечание 1. Знаменатель левой части формулы (1) отличен от нуля. В противном случае к функции 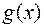можно было бы применить теорему Ролля и внутри получить точку, в которой 
, что противоречит условию теоремы Коши.
Замечание 2. Может показаться, что теорема Коши не содержит ничего нового: ведь к каждой из функций и 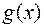можно применить формулу конечных приращений (2) из §2. Однако, теорема Лагранжа не гарантирует, что точка 
одна и та же для различных функций.
