I. Если 
, то 
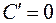(производная постоянной функции равна 0).
II. Если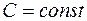 
, а 
– дифференцируема в точке x, то 
(постоянный множитель можно вынести за знак производной).
III–V. Если функции 
и 
дифференцируемы в точке x, то их сумма, разность, произведение и частное (если 
) также дифференцируемы в этой точке, причем имеют место формулы:
III. 
IV. 
V. 
Докажем, например, формулу дифференцирования частного. Пусть 
. Тогда:
.
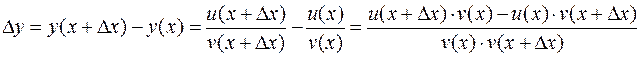Добавим и вычтем в числителе член 
, сгруппируем и вынесем за скобки общие множители. Будем иметь:
.
Составим разностное отношение, т.е. отношение приращения функции к приращению аргумента:
.
Теперь перейдем к пределу при 
. Так как 
и 
- дифференцируемы (а, следовательно, непрерывны), то существуют пределы
, 
, 
,
а и от 
не зависят и выносятся за знаки пределов. Значит, существует предел разностного отношения, т.е.
.
VI. Пусть функция 
дифференцируема в точке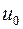 
, а функция 
дифференцируема в точке 
, причем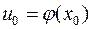 
. Тогда и сложная функция 
дифференцируема в точке и имеет место формула
.
Другие формы записи этой формулы:
, 
.
Для доказательства придаем аргументу x функции приращение . Оно вызовет приращение 
этой функции, которое в свою очередь вызовет приращение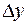 
функции . В силу теоремы 1 §4 из диффе-ренцируемости функций 
и 
имеем:
Подставляя первую формулу во вторую, получим для приращения сложной функции:
Сразу отметим, что в силу непрерывности функции (следует из её дифференцируемости) ее приращение стремится к нулю при . Составляем разностное отношение и переходим к пределу
.
Первое слагаемое под знаком предела в правой части – это постоянная. Второе – произведение постоянной на бесконечно малую, ибо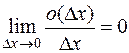 
по определению символа 
. Третье слагаемое представим в виде
.
Здесь первый множитель есть бесконечно малая при , а второй имеет конечный предел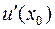 
. Итак, второе и третье слагаемое – это бесконечно малые при . Отсюда и получаем формулу дифференцирования сложной функции.
Замечание 1. Остальные правила дифференцирования приведем позже.
