Очевидно, что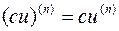 
и 
. Для производной
n -го порядка от произведения функций имеется т.н. формула Лейбница. Приведем ее без доказательства:
, где 
.
Заметим, что под производной нулевого порядка принято понимать саму
функцию: 
.
IV Функция, заданная параметрически
Пусть функция задана параметрическими уравнениями
Её первая производная – это также функция, заданная параметрически:
Тогда
Пример. Для 
первая производная имеет вид 
Тогда 
и вторая производная такова: 
V Функция, заданная неявно
Повторное дифференцирование такой функции покажем на примере:
Тогда по определению:
.
Остается подставить в последнее выражение значение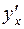 
:
.
Полученное выражение можно упростить, используя само уравнение:
.
Тема ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Лекция 10
