VII Логарифмическая производная
Пусть функция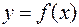 
положительна и дифференцируема. Тогда и функция 
– дифференцируема, причем
.
Это выражение и называется логарифмической производной функции 
. Отсюда легко получить производную самой функции :
.
Используя эту формулу можно получить правило дифференцирования сложной степенно-показательной функции:
.
Окончательно имеем формулу:
.
Замечание 2. Вообще говоря, всегда лучше помнить не лишнюю формулу, а приём, который приводит к этой формуле. Для степенно-показательной функции можно предложить прием, использующий основное логарифмическое тождество:
.
Примеры.
2. 
VIII Дифференцирование обратной функции
Пусть функция 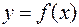в некоторой окрестности точки 
– непрерывная и строго монотонная, а кроме того, дифференцируема в точке , причем 
. Тогда в некоторой окрестности точки 
существует обратная функция 
, также непрерывная, строго монотонная и дифференцируемая в точке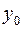 
, причем
. (1)
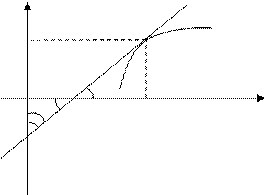
Строгое доказательство приводить не будем, но дадим геометрическую иллюстрацию. При этом используем тот факт, что у графики взаимно-обратных функци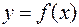й и совпадают, а производная – это угловой коэффициент касательной.
 |
,
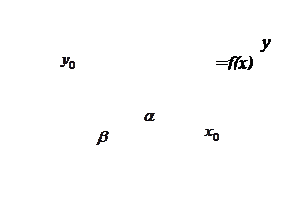
Формулу (1) записывают еще в виде 
или 
.
Применим последнюю формулу для вычисления производной, например, арксинуса:
,
IX Дифференцирование функции, заданной параметрически
Пусть имеется система параметрических уравнений 
, 
, причем функции 
и 
дифференцируемы и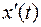 
сохраняет знак. Тогда на области значений функции существует дифференцируемая функция 
, причем
Действительно, из условия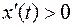 
(или 
) следует монотонность функции 
; следовательно, у неё существует обратная 
. Тогда 
– некоторая функция от x. Её производную можно найти, если применить правила дифференцирования сложной и обратной функций:
Пример. 3. Составим уравнение касательной к эллипсу 
в точке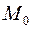 
, соответствующей значению параметра 
.
Координаты точки касания: 
, 
. Угло-
вой коэффициент касательной
.
Искомое уравнение имеет вид: 
.
Замечание 3. Вообще говоря, производная функции, заданной параметрически, есть функция, заданная параметрически. Методически более правильным было бы писать такую производную в виде системы параметрических уравнений:
X Дифференцирование функции, заданной неявно
При некоторых условиях, которые будут сформулированы в теме “Функции нескольких переменных”, уравнение с двумя переменными вида 
определяет y как функцию от x: 
. Другими словами, существует функция 
, обращающая уравнение в тождество. Производную этой функции можно найти (в неявном же виде), не находя самой функции. Точные формулы будут даны позже, а сейчас сформулируем правило:
тождество 
дифференцируем по x, не забывая, что y – это функция от x; затем из полученного равенства находим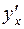 
.
Примеры. 4. Дано: 
. Дифференцируем по x обе части:
. 
.
5. Выведем уравнение касательной к эллипсу 
, проходящей через его точку 
. Найдем угловой коэффициент касательной. Для этого уравнение эллипса дифференцируем по x, не забывая, что :
.
В общее уравнение касательной подставим найденный коэффициент и преобразуем уравнение:
.
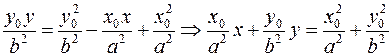Так как точка 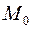принадлежит эллипсу, то правая часть полученного уравнения равна 1. Следовательно, искомая касательная имеет уравнение
.
