Теорема Ролля. Пусть функция 
удовлетворяет условиям: 1) непре- рывна на 
; 2) дифференцируема на 
; 3) 
. Тогда существует точка 
такая, что 
.
Доказательство. В силу непрерывности функции на замкнутом промежутке существуют точки 
такие, что 
, 
и, поэтому 
.
Для этих точек имеется 2 возможности: 1) они совпадают с концами промежутка; 2) хотя бы одна из них является внутренней точкой.
В первом случае из следует, что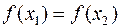 
, то есть 
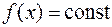. Поэтому, 
.
Во втором случае, точка 
или 
, попавшая внутрь промежутка, является точкой экстремума функции и так как дифференцируема в этой точке, то по теореме Ферма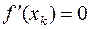 
.
Обе возможности приводят к тому, что внутри существует точка c, в которой .
Замечание 1. На геометрическом языке теорема Ролля означает следующее: если крайние ординаты кривой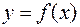 
равны, то на кривой найдется точка, где касательная параллельна оси Ox. При этом требования непрерывности функции на и дифференцируемости на существенны и не могут быть ослаблены.
Теорема Лагранжа. Пусть функция непрерывна на и дифференцируема на . Тогда существует точка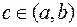 
такая, что справедлива формула:
. (1)
Доказательство. Введем вспомогательную функцию 
, определив её на равенством:
.
Эта функция, так же как и , удовлетворяет первым двум условиям теоремы Ролля. Подберем l так, чтобы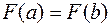 
(третье условие теоремы Ролля):
.
Теперь к функции можно применить теорему Ролля: 
и 
: 
, т.е.
.
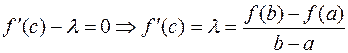Теорема доказана.
Замечание 2. Теорему Лагранжа называют основной теоремой дифференциального исчисления, а формулу (1), записанную в виде
, (2)
называют формулой конечных приращений. Положим 
, а точку c, лежащую между x и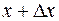 
запишем в виде 
, где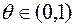 
. Тогда:
.
Эта формула даёт точное значение для приращения функции при любых конечных приращениях аргумента. Этим она отличается от формулы бесконечно малых приращений (§4, тема “Производная”)
,
из которой получается лишь приближенное равенство
,
справедливое для достаточно малых 
.
Замечание 3. Пусть 
. Тогда правая часть формулы (1) есть угловой коэффициент секущей AB. Геометрически теорема Лагранжа означает следующее: на графике функции 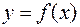между точками А и В найдется точка 
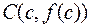, касательная в которой параллельная секущей AB.
Несмотря на то, что в формуле конечных приращений фигурирует неизвестное число с (или 
), эта формула имеет многочисленные приложения.
Пример 1. Доказать оценку
.
Для доказательства рассмотрим функцию 
. Тогда
, 
.
Значит,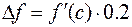 
, где 
. Оценим производную функции
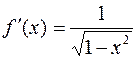в точке с:
.
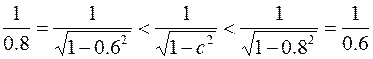Умножая все части этого двойного неравенства на 0.2, получим:
.
Пример 2. Формула (1) позволяет доказывать некоторые полезные неравенства. Например,
, 
,
так как 
. Или
, если только 
: для 
.
Лекция 11
