I Определение и геометрический смысл
Известно, что приращение дифференцируемой в точке  функции
функции 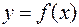 можно записать в виде суммы
можно записать в виде суммы

двух слагаемых, каждое из которых стремится к нулю при  . Однако, второе слагаемое имеет порядок малости более высокий, чем первое (“быстрее” стремится к нулю). То есть в этой сумме главную роль играет первое слагаемое.
. Однако, второе слагаемое имеет порядок малости более высокий, чем первое (“быстрее” стремится к нулю). То есть в этой сумме главную роль играет первое слагаемое.
Определение. Главная часть приращения 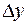 функции
функции 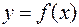 , линейная относительно приращения
, линейная относительно приращения  аргумента x, называется дифференциалом функ-ции и обозначается символом dy.
аргумента x, называется дифференциалом функ-ции и обозначается символом dy.
Итак, 
 .
.
Геометрический смысл виден из рисунка: дифференциал функции – это приращение ординаты касательной к графику функции, соответствующее приращению аргумента  .
.
Дифференциалом независимой переменной x, принято называть ее приращение  и обозначать dx:
и обозначать dx:  . Тогда формула для дифференциала функции приобретает симметричный вид
. Тогда формула для дифференциала функции приобретает симметричный вид
 или
или  .
.
II Инвариантность формы первого дифференциала
Правило дифференцирования сложной функции приводит к одному очень важному свойству дифференциала. Вычислим dy для функции  в двух случаях:
в двух случаях:
1) x – независимая переменная, тогда  ;
;
2) x – некоторая функция  , тогда
, тогда

Сравнивая результаты, получаем т.н. свойство инвариантности формы первого дифференциала:
форма 1го дифференциала функции  не зависит от того, является
не зависит от того, является
ли переменная x независимой или функцией другой переменной.
III Таблица дифференциалов
Так как дифференциал dy лишь множителем dx отличается от производной 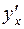 , то по таблице производных легко составить таблицу дифференциалов.
, то по таблице производных легко составить таблицу дифференциалов.
1.  ,
,  ,
,  .
.
2.  ,
,  .
.
3.  ,
, 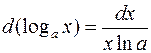 .
.
4.  . 5.
. 5.  .
.
6. 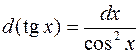 . 7.
. 7. 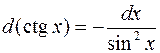 .
.
8.  . 9.
. 9.  .
.
10. 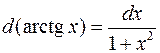 . 11.
. 11.  .
.
Также легко получить формулы для дифференциалов суммы, разности, произведения и частного функций:
а) 
б) 
в) 
Отметим, что в таблице дифференциалов переменная x может быть как независимой, так и некоторой функцией. В таблице же производных (§6) x – это только независимая переменная.
Замечание. Формула для дифференциала функции 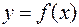 , а именно:
, а именно:
 ,
,
позволяет написать формулу, выражающую производную функции через дифференциалы dx и dy:
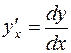 .
.
При этом такая формула сохраняет силу, по какой бы независимой переменной ни были вычислены dx и dy. Эта формула позволяет легко запоминать (но не доказывать!) некоторые правила дифференцирования:
для сложной функции 
 ;
;
для обратной функции
 ;
;
для функции, заданной параметрически 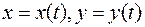
 .
.






