I Определение и обозначения
Если функция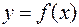 
дифференцируема на некотором промежутке, то её производная 
сама является функцией, определенной на этом промежутке. Следовательно, по отношению к ней можно ставить вопрос о существовании и нахождении производной. Если она существует, то её называют второй производной (или производной 2го порядка), и обозначают одним из символов
.
Аналогично, если существует производная от второй производной, то её называют третьей производной и обозначают, например, 
.
Вообще, производной n -го порядка называют производную от производной (n– 1)-го порядка и обозначают 
. Итак, по определению
.
II Производные некоторых функций
1. y= sin x, y= cos x
Первые производные этих функций 
и формулы приведения 
позволяют методом математической индукции получить выражения для производных n -го порядка:
.
2. y=xa
Если 
, то, последовательно дифференцируя, получим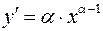 
, 
, и вообще:
.
Если же показатель степени натуральный, то:
3. y=ax
, в частности, 
, 
.
4. y= ln x
,
.
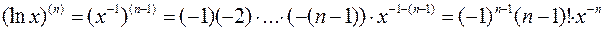