Рассмотрим функцию 
, определенную в точке 
и в некоторой ее окрестности. Придадим аргументу x приращение 
, не выводящее аргумент за пределы окрестности. Функция получит приращение 
.
Определение. Предел отношения приращения функции 
к приращению аргумента при 
(если этот предел существует) обозначается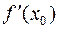 
и называется производной функции 
по переменной в x точке x 0.
Итак, по определению
.
Из определения следует, что производная – это число. Однако чаще всего оказывается, что это число можно вычислить не только в одной точке x 0, а во всех точках некоторого интервала. Тем самым на этом интервале определяется некоторая новая функция, которая тоже называется производной функции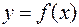 
и обозначается: 
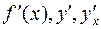. Кроме этих обозначений используются и другие:
– производная как функция (читается “дэ игрек по дэ икс”),
– производная в фиксированной точке x 0.
Сравнивая результаты, полученные в §1, с определением производной, можно придать производной смысл:
1) если 
– закон движения, то 
;
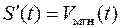2) 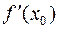– это угловой коэффициент (тангенс угла наклона к оси Ox) касательной к графику функции 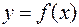в точке с абсциссой x 0.
Используя 2) легко написать уравнение касательной:
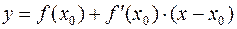
и нормали, т.е. прямой, проходящей через точку касания перпендикулярно касательной:
.
Пример. Вычислить (по определению) производную функции 
.
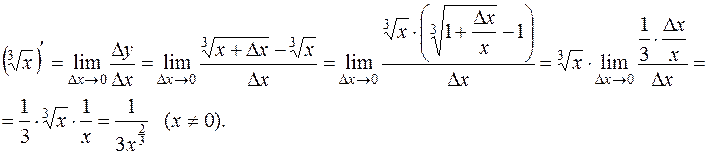
Замечание 1. Производную 
удобно понимать как скорость изменения функции относительно аргумента x.
Замечание 2. Отношение приращения функции к приращению аргумента называют разностным отношением функции.
