Запишем уравнения Максвелла для данного случая:
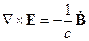(2)
(3)
и уравнение связи 
. Если сторонних токов нет, то можно ещё привлечь закон Ома 
.
Из (2) и (3) получим волновые уравнения. Подействуем операторами:
на (2)
на (3)
тогда получаем:
(4)
(5)
Правая часть в выражении (4) и левая часть в выражении (5) совпадают, тогда:
(6)
(6) удобно записать в виде:
где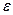 
- некоторый тензор.
Распишем в компонентах:
, тогда
где оператор 
- тензорный, дифференциальный оператор, он учитывает пространственную дисперсию.
Любое поле можно разложить по плоским монохроматическим волнам. Тогда решение уравнения сводится к нахождению и рассмотрению плоских монохроматических волн, этим плоским монохроматическим волнам соответствуют поля следующего типа:
Разложение в ряд Фурье:
Операторы заменяем по правилу:
Последнее правило действует в случае плоских монохроматических волн. Тогда имеем выражение:
Здесь введён тензор 
, который определяется следующим образом:
Решение уравнения зависит и от оператора в левой части, и от правой части. При 
мы имеем в решении нормальные волны (эти волны идут без источников).
