-уравнение Гельмгольца
в правой части этого уравнения – источник 
, в левой – поле 
источника .
, 
Для нахождения решения уравнения Гельмгольца вводят функцию Грина, удовлетворяющую условию:
Здесь надо использовать разложение функции Грина в интеграл Фурье:
где 
Для 
-функции:
Подействуем на функцию Грина оператором 
:
Используем то, что 
, а следовательно 
:
Тогда перепишется в виде:
Равенство этих интегралов приводит к равенству фурье-образов:
Тогда фурье-образ функции Грина:
Теперь надо найти оригинал. Используем для этого теорию вычетов:
Пусть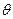 
- угол между 
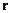и 
. Обозначим 
. Введём сферические переменные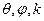 
.
, тогда 
.Следовательно 
Используем теорию вычетов. У этого интеграла есть два полюса: 
и 
. Надо использовать при расчёте полюс , чтобы получить физически обоснованную асимптотику.
Переходим в комплексную плоскость, замыкаем контур обхода сверху. Используем фиктивный переход:
Это позволяет получить нужную асимптотику.
- функция Грина уравнения Гельмгольца
Обозначим 
