В случае плоских волн эти функции есть функции аргументов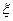 
и 
; 
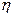- нормаль к поверхности фронта волны.
, 
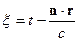
Вектор 
- волновой вектор, где 
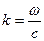- волновое число. Запишем соотношения:
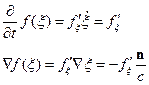
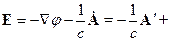
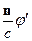
Первое слагаемое содержит и поперечную и продольную составляющую. Второе слагаемое приводит к продольной составляющей. Чтобы в поле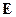 
не было продольных составляющих надо положить 
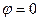и надо 
, т.е. чтобы поле было только поперечным нужно ввести калибровку:
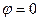
Вообще-то следует из уравнения Максвелла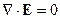 
.
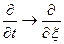
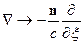
Рассмотрим теперь:
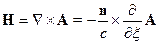
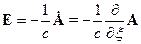
Тогда:
Т.е. 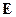и 
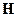ортогональны. Более того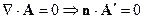 
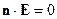
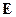Т.е. и ортогональны. В результате образовалась правая тройка векторов. Ортогональность вектора векторам 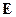и 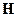означает поперечность волны.
Рассмотрим вектор Пойнтинга:
Для поперечных волн , тогда:
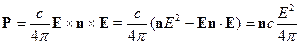
Найдём выражение для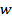 
, выраженное через одно из полей:
Тогда
Связь вектора Пойнтинга с плотностью энергии:
Значит, 
направлен по вектору нормали распространения фронта волны
