Запишем уравнение Даламбера:
ð 
где 
, а 
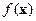- источники.
Под 
понимаем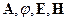 
Под 
понимаем 
, 
Т.к. любое поле раскладывается по плоским монохроматическим волнам, то мы будем решение уравнения Даламбера искать в виде:
Значит 
, где 
- волновое число.
Тогда:
ð 
Т.е. оператор Даламбера переходит в оператор Гельмгольца. Тогда:
(**)
Если источник 
, тогда решение имеет вид 
..
В общем случае можно записать разложение через интеграл Фурье:
Решение (**) можно записать через функцию Грина:
Здесь первое слагаемое – частное решение неоднородного уравнения(представляет большой интерес, т.к. здесь стоят источники поля 
). Второе слагаемое – общее решение однородного уравнения.
Функция Грина 
, тогда:
ð 
Мы будем рассматривать случай неограниченного пространства, где:
Временно введём обозначение: 
, тогда 
. Функцию Грина можно разложить в интеграл Фурье:
; 
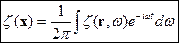
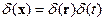Тогда 
- есть функция Грина уравнения Гельмгольца. Т.е. получается, что фурье-образ функции Грина уравнения Даламбера есть функция Грина уравнения Гельмгольца.
Теперь получим полное выражение для функции Грина уравнения Даламбера:
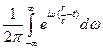- это разложение в интеграл Фурье 
-функции, где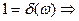 
Мы получили разложение функции Грина для уравнения Даламбера. Это запаздывающая функция Грина.
Запаздывающая функция Грина удовлетворяет принципу причинности.
Делаем обратную замену, т.е. 
и 
, 
:
, где 
В силу свойства -функции при 
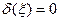, тогда решение приобретает физический смысл при 
.
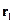- точка источника.
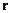- точка наблюдателя.
За какое время дойдёт сигнал из 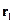в 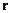, если сигнал распространяется со скоростью 
:
Чтобы информация от источника попала вовремя к наблюдателю нужно, чтобы
В этом и есть физический смысл , для которого удовлетворяется принцип причинности.
